1 领域不变的表征
在迁移学习/领域自适应中,我们常常需要寻找领域不变的表征(Domain-invariant Representation)[1],这种表示可被认为是学习到各领域之间的共性,并基于此共性进行迁移。而获取这个表征的过程就与深度学习中的“表征学习”联系紧密[2]。生成模型,自监督学习/对比学习和最近流行的因果表征学习都可以视为获取良好的领域不变表征的工具。
2 生成模型的视角
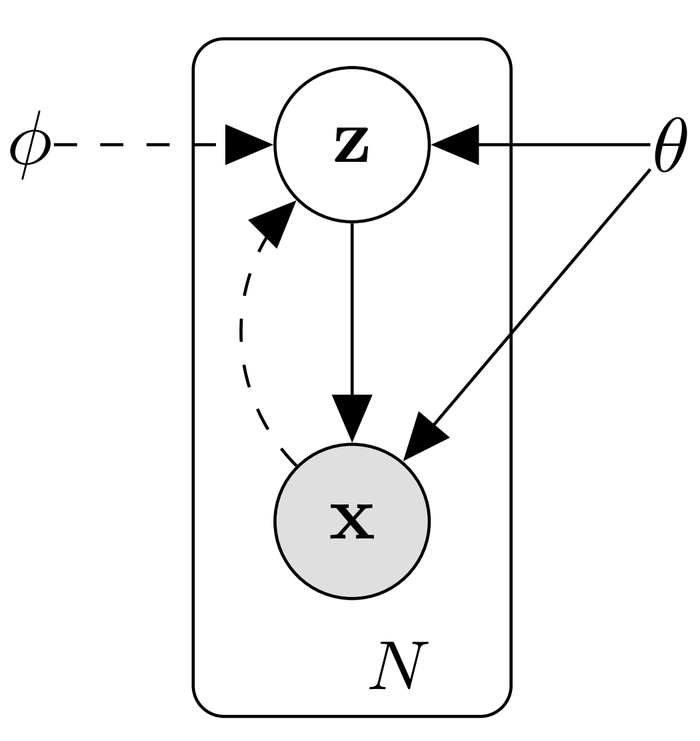
生成模型的视角是在模型中引入隐变量(Latent Variable),而学到的隐变量为数据提供了一个隐含表示(Latent Representation)。如下图所示[3],生成模型描述了观测到的数据\(\mathbf{x}\)由隐变量\(\mathbf{z}\)的一个生成过程:
也即
\]
求和(或积分)项\(\sum_{\mathbf{z}}p_{\boldsymbol{\theta}}(\mathbf{z})p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})\)常常难以计算,而且\(\mathbf{z}\)的后验分布\(p_{\boldsymbol{\theta}}(\mathbf{z}|\mathbf{x})=p_{\boldsymbol{\theta}}(\mathbf{x} \mid \mathbf{z}) p_{\boldsymbol{\theta}}(\mathbf{z}) / p_{\boldsymbol{\theta}}(\mathbf{x})\)也难以计算,导致EM算法不能使用。
VAE的思想是既然后验\(p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})\)难以进行推断,那我们可以采用其变分近似后验分布\(q_\phi(\mathbf{z} \mid \mathbf{x})\)(对应重参数化后的编码器),而数据的生成过程\(p_{\boldsymbol{\theta}}(\mathbf{x} \mid \mathbf{z})\)则视为解码器。如下图所示。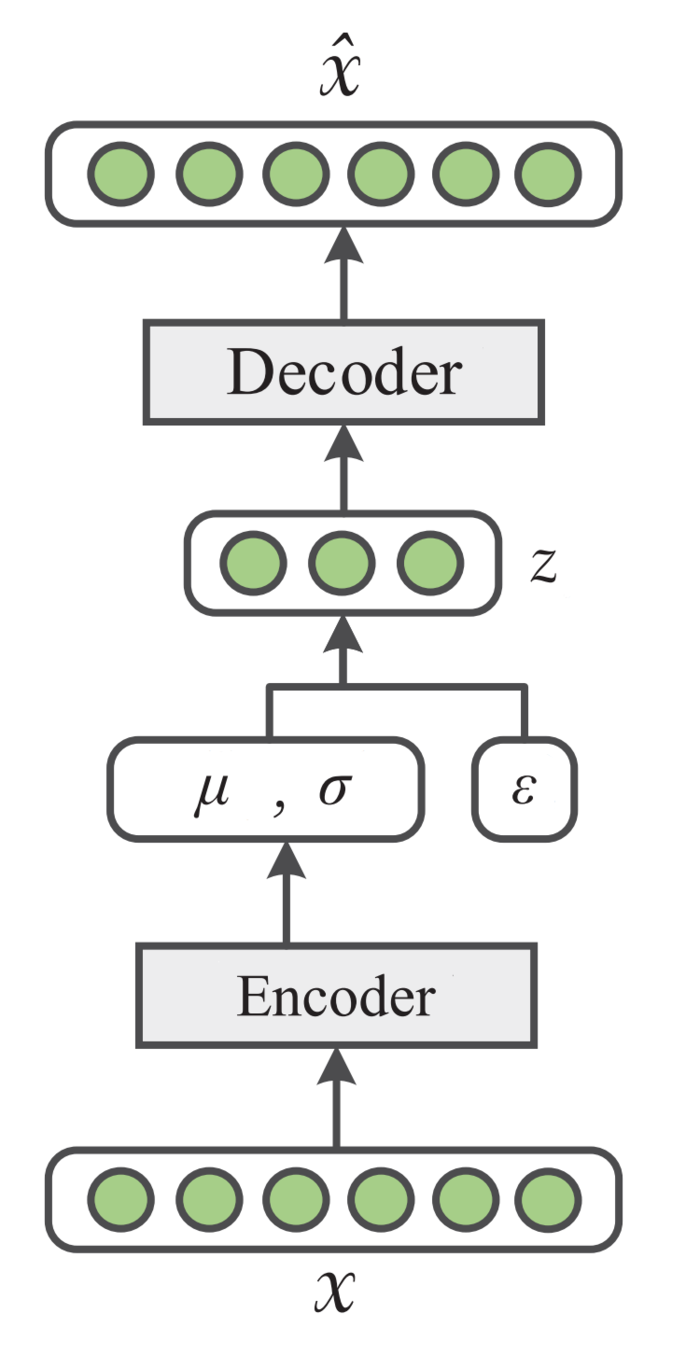
变分自编码器的优化目标为最大化与数据点\(x\)相关联的变分下界:
\widetilde{\mathcal{L}}_{\mathrm{VAE}}(\mathbf{x} ; \theta, \phi)
&=-D_{K L}\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p_\theta(\mathbf{z})\right)+ \mathbb{E}_{\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x})} \log p_\theta(\mathbf{x} \mid \mathbf{z}) \\
& \leqslant \log p_{\boldsymbol{ \theta}}(\mathbf{x})
\end{aligned}
\]
上面的第一项使近似后验分布\(q(\mathbf{z}|\mathbf{x})\)和模型先验\(p_{\boldsymbol{\theta}}(\mathbf{z})\)(一般设为高斯)尽可能接近(这样的目的是使解码器的输入尽可能服从高斯分布,从而使解码器对随机输入也有很好的输出);第二项即为解码器的重构对数似然。
接下来我们说一下如何从近似后验分布\(q(\mathbf{z}|\mathbf{x})\)中采样获得\(\mathbf{z}\),因为这\(\mathbf{z}\)不是由一个函数产生,而是由一个随机采样过程产生(它的输出会随我们每次查询而发生变化),故直接用一个神经网络表示\(\mathbf{z} = g(\mathbf{x})\)是不行的,这里我们需要用到一个重参数化技巧(reparametrization trick):
& \mathbf{z} = g_{\phi}(\epsilon, \mathbf{x})=\mathbf{\mu} + \mathbf{\sigma}\odot\mathbf{\epsilon} \\
& \mathbf{\mu},\mathbf{\sigma} = \text{Encoder}_{\phi}(x)\\
& \mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})
\end{aligned}
\]
这样我们即能保证\(\mathbf{z}\)来自随机采样的要求,也能通过反向传播进行训练了。
这里提一下条件变分自编码器[4],它在变分自编码器的基础上增加了条件信息\(\mathbf{c}\)(比如数据\(\mathbf{x}\)的标签信息),如下图所示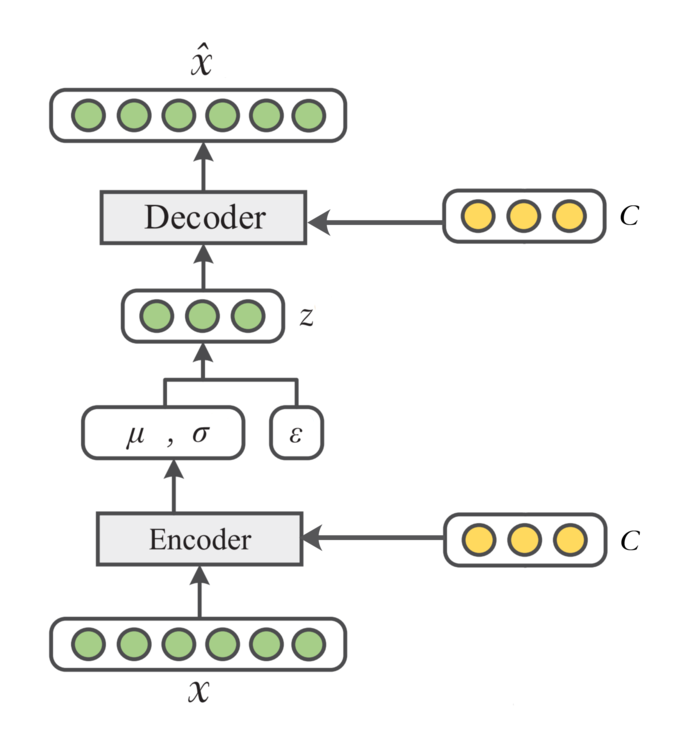
变分自编码器所要最大化的函数可以表示为:
\widetilde{\mathcal{L}}_{\mathrm{CVAE}}(\mathbf{x}, \mathbf{c} ; \theta, \phi) &=-D_{K L}\left(q_\phi(\mathbf{z} \mid \mathbf{x}, \mathbf{c}) \| p_\theta(\mathbf{z} \mid \mathbf{c})\right)+\mathbb{E}_{\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x}, \mathbf{c})}\log p_\theta(\mathbf{x} \mid \mathbf{z}, \mathbf{c})\\
& \leqslant \log p_{\boldsymbol{ \theta}}(\mathbf{x|\mathbf{c}})
\end{aligned}
\]
关于自编码器和变分自编码在MNIST数据集上的代码实现可以参照GitHub项目[5]。
训练完成后,VAE的隐向量\(\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x})\)和CVAE的隐向量\(\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x}, \mathbf{c})\)的对比如下:
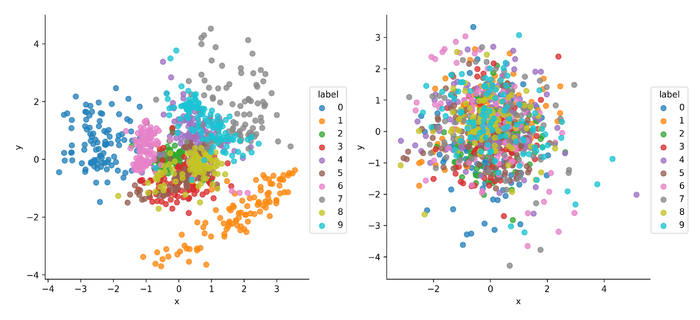
可以看到CVAE的隐空间相比VAE的隐空间并没有编码标签信息,而是去编码其它的关于数据\(\mathbf{x}\)的分布信息,可视为一种解耦表征学习(disentangled representation learning)技术。
就我们的迁移学习/领域自适应任务而言,训练生成模型获得了隐向量之后就已经完成目标,之后可以将隐向量拿到其它领域的任务中去用了。不过有时训练生成模型的最终目的还是为了生成原始数据。接下来我们来对比两者的图像生成效果。移除编码器部分,随机采样\(\mathbf{z}\),VAE的生成\(p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})\)和CVAE的生成\(p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z}, \mathbf{c})\)如下图所示,其中CVAE会将图像的标签信息\(\mathbf{c}\)做为解码器的输入。
可以看到其中所编码的标签信息发挥的重要作用。
这里补充一下,提取领域不变的表示也可以通过简单的特征提取器+GAN对抗训练机制来得到。如在论文[6]中,设置了一个生成器根据随机噪声和标签编码来生成“伪”特征,并训练判别器来区分特征提取器得到的特征和“伪”特征。此外,作者还采用了随机投影层来使得判别器更难区分这两种特征,使得对抗网络更稳定。其架构如下图所示:

2 自监督学习/对比学习的视角
在自监督预训练中,其实也可以看做是在学习\(p(\mathbf{x})\)的结构,我们要求该过程能够学习出一些对建模\(p(\mathbf{y}|\mathbf{x})\)(对应下游的分类任务)同样有用的特征(潜在因素)。因为如果\(\mathbf{y}\)与\(\mathbf{x}\)的成因之一非常相关,那么\(p(\mathbf{x})\)和\(p(\mathbf{y}|\mathbf{x})\)也会紧密关联,故试图找到变化潜在因素的自监督表示学习会非常有用。自然语言处理中的经典模型BERT[7]便是基于自监督学习的思想。
而对比学习也可以视为自监督学习的一种,它是通过构造锚点样本、正样本和负样本之间的关系来学习表征。对于任意锚点样本\(\mathbf{x}\),我们用\(\mathbf{x}^+\)和\(\mathbf{x}^-\)分别表示其正样本和负样本,然后\(f(\cdot)\)表示要训练的特征提取器。此时,学习目标为限制锚点样本与负样本之间的距离远大于其与正样本之间的距离(此处的距离为在表征空间的距离),即:
\]
其中,\(d(\cdot, \cdot)\)为一可定制的距离度量函数,常用的是如下的余弦相似度:
\]
当向量\(\mathbf{a}\)、\(\mathbf{b}\)归一化后,余弦相似度等价于向量内积。此外,互信息也可以作为相似度的度量。
在经典的SimCLR[8]架构按照如下图所示的图像增强(比如旋转裁剪等)方式产生正样本: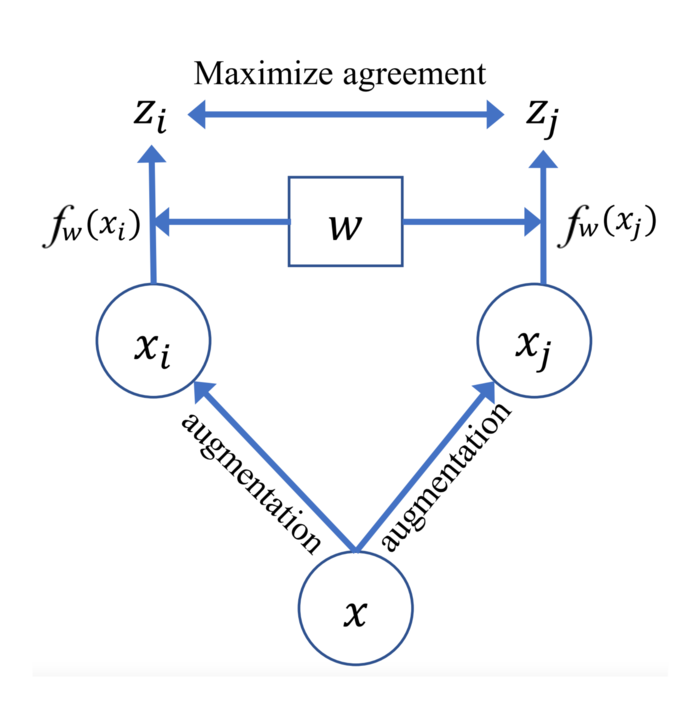
如上图所示,它对每张输入的图片进行两次随机数据增强(如旋转剪裁等)来得到\(\mathbf{x}_i\)和\(\mathbf{x}_j\)。对于\(\mathbf{x_i}\)而言,\(\mathbf{x}_j\)为其配对的正样本,而其它\(N-1\)个样本则视为负样本。
对比学习损失函数InfoNCE如下所示:
\]
这里\(\mathbf{x}_j\)表示第\(j\)个负样本。
对比学习一般也是用来获取embeddings,然后用于下游的有监督任务中,如下图所示[9]:

3 因果推断的视角
前面我们提到在对比学习中可以运用数据增强来捕捉域不变特征,然而这种数据增强的框架也可以从因果表征学习的视角来看。因果推断中的因果不变量同样也可以对应到领域不变的表征。
如今年CVPR 22的一篇论文[10]所述,原始数据\(X\)由因果因子\(S\)(如图像本身的语义)和非因果因子\(U\)(如图像的风格)混合决定,且只有\(S\)能够影响原始数据的类别标签。注意,我们不能直接将原始数据量化为\(X=f(S, U)\),因为因果因子/非因果因子一般不能观测到并且不能被形式化。
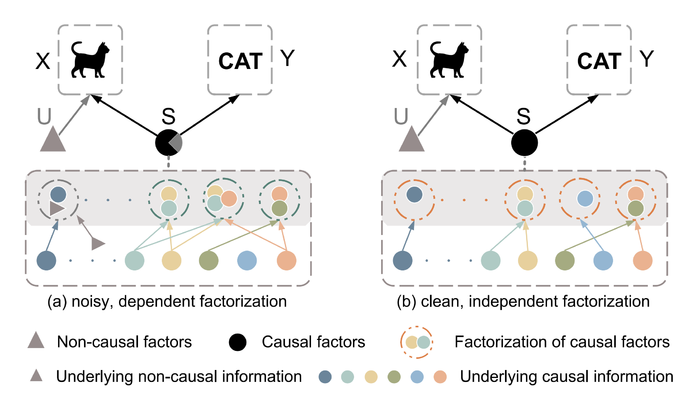
这里的任务为将因果因子\(S\)从原始数据中提取出来,而这可以在因果干预\(P(Y\mid do(U), S)\)的帮助下完成,具体的措施类似于我们前面所说的图像增强,如下图所示:
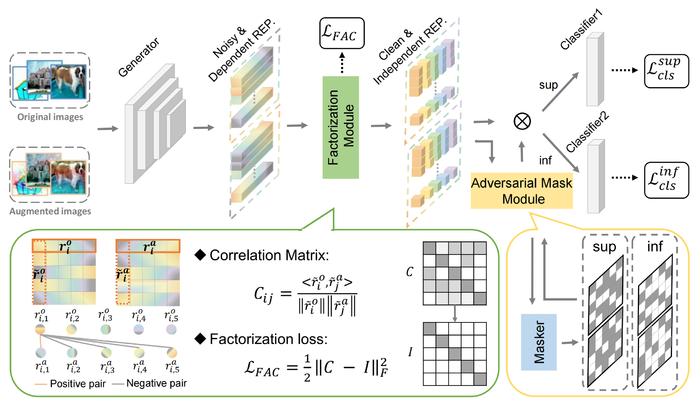
如图,论文对非因果因子采用因果介入来生成增强后的图像,然后将原始和增强图像的表征送到因子分解模块,该模块使用分解损失函数来迫使图像表征和非因果因子分离。最后,通过对抗掩码模块让生成器和掩码器之间形成对抗,使得表征更适用于之后的分类任务。
参考
- [1] 王晋东,陈益强. 迁移学习导论(第2版)[M]. 电子工业出版社, 2022.
- [2] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.
- [3] Kingma D P, Welling M. Auto-encoding variational bayes[C]. ICLR, 2014.
- [4] Sohn K, Lee H, Yan X. Learning structured output representation using deep conditional generative models[J]. Advances in neural information processing systems, 2015, 28.
- [5] https://github.com/timbmg/VAE-CVAE-MNIST
- [6] Zhang L, Lei X, Shi Y, et al. Federated learning with domain generalization[J]. arXiv preprint arXiv:2111.10487, 2021.
- [7] Devlin J, Chang M W, Lee K, et al. Bert: Pre-training of deep bidirectional transformers for language understanding[J]. NAACL, 2018.
- [8] Chen T, Kornblith S, Norouzi M, et al. A simple framework for contrastive learning of visual representations[C]//International conference on machine learning. PMLR, 2020: 1597-1607.
- [9] Jaiswal A, Babu A R, Zadeh M Z, et al. A survey on contrastive self-supervised learning[J]. Technologies, 2020, 9(1): 2.
- [10] Lv F, Liang J, Li S, et al. Causality Inspired Representation Learning for Domain Generalization[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 8046-8056.
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:寻找领域不变量:从生成模型到因果表征 - Python技术站


 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫