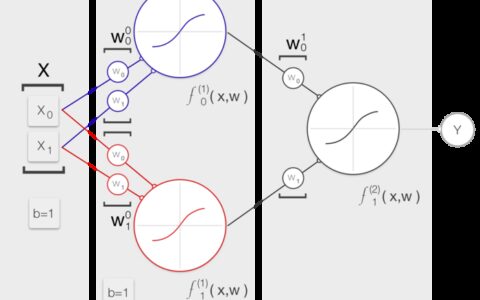
牛顿法解最大似然估计
对于之前我们解最大似然估计使用了梯度下降法,这边我们使用牛顿法,速度更快。
具体看这个图
下面在原理上说一说。
摘自:http://blog.csdn.net/luoleicn/article/details/6527049
对于一个目标函数f,求函数f的极大极小问题,可以转化为求解函数f的导数f'=0的问题,这样求可以把优化问题看成方程求解问题(f'=0),为了求解f'=0的根,把f(x)的泰勒展开,展开到2阶形式:
这个式子是成立的,当且仅当 Δx 无线趋近于0。此时上式等价与:
求解:
得出迭代公式:
一般认为牛顿法可以利用到曲线本身的信息,比梯度下降法更容易收敛(迭代更少次数),如下图是一个最小化一个目标方程的例子,红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
在上面讨论的是2维情况,高维情况的牛顿迭代公式是:
其中H是hessian矩阵,定义为:
高维情况依然可以用牛顿迭代求解,但是问题是Hessian矩阵引入的复杂性,使得牛顿迭代求解的难度大大增加,但是已经有了解决这个问题的办法就是Quasi-Newton methond,不再直接计算hessian矩阵,而是每一步的时候使用梯度向量更新hessian矩阵的近似。
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:深度学习5牛顿法 - Python技术站















 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫