(未更完)
我算法中也就差点数论没学了,这几周卷了,学了一下,分享一下啊。
我会讲得详细一点,关于我不懂得地方,让新手更容易理解。
学习反演有很多定义啥的必须要记的,学的时候容易崩溃,所以希望大家能坚持下来。
第一个定义:
$\lfloor x\rfloor$:意思是小于等于 $x$ 的最大整数。
数论分块
学习反演之前,要先学习一些边角料,先来看数论分块(又名整除分块)。
最典型的一个例子是求 $\sum\limits_{i=1}^n \lfloor\frac{n}{i}\rfloor$,其中 $n\leq 10^{12}$。
首先,一个个循环 $i$ 显然会超时,所以考虑优化这个方法。
通过打表可以发现 $\lfloor\frac{n}{i}\rfloor$ 中有大部分值是相等的,且值的个数不超过 $2\sqrt{n}$。
函数图像长这样:
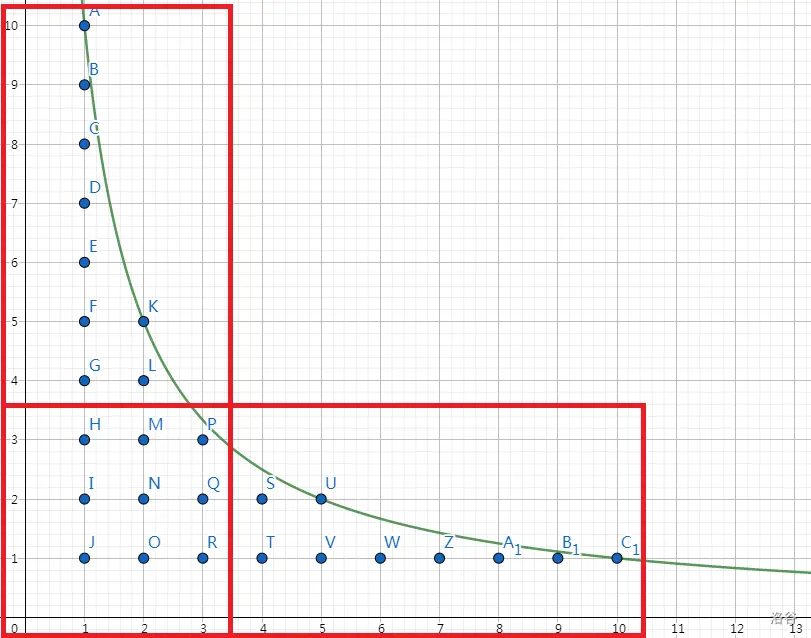
下面来证明一下:
当 $i\leq \sqrt{n}$ 时:$i$ 的取值一共 $\sqrt{n}$,所以不同的值不会超过 $\sqrt{n}$。
当 $i\geq \sqrt{n}$ 时:$\lfloor\frac{n}{i}\rfloor\leq\sqrt{n}$,所以不同的值也不会超过 $\sqrt{n}$。
那么就可以枚举 $\lfloor\frac{n}{i}\rfloor$ 的值来 $\sqrt{n}$ 计算了。
具体怎么做呢,我们发现值相同的数成块状分布,假如知道块的第一个是 $l$,那么块的最后一个就是 $n / (n / l)$(这里默认下取整)。
这个结论模拟一下就能懂,并且很好背。
代码(现场写的):
for (int l = 1, r; l <= n; l = r + 1) { r = n / (n / l); ans += (n / l) * (r - l + 1); }
居然有个板子题,还是绿的:链接,别忘了开 $LL$ 啊。
数论分块的变形
形式一:
求 $\sum\limits_{i=1}^n$ $k$ $mod$ $i$。
显然:$k$ $mod$ $i=k-i\cdot\lfloor\frac{k}{i}\rfloor$。
化为:$\sum\limits_{i=1}^n$ $k-i\cdot\lfloor\frac{k}{i}\rfloor$。
$k$ 和循环内的变量无关,把它提出来得到:$n\cdot k-\sum\limits_{i=1}^ni\cdot\lfloor\frac{k}{i}\rfloor$
$\sum$ 里面的使用整除分块。这个整除分块怎么做呢?
在枚举 $\lfloor\frac{k}{i}\rfloor$ 时,假如一个块的左区间是 $l$,右区间是 $r$。
因为这一段 $\lfloor\frac{k}{i}\rfloor$ 的值相同,所以设它为 $x$
那么这一段的贡献就是 $l\cdot x + (l+1)\cdot x + (l+2)\cdot x +...+ r\cdot x$,
把 $x$ 提出来再用等差数列求和公式得到:
$(l + r) * (r - l + 1) / 2 * x$。另外注意 $\lfloor\frac{k}{l}\rfloor=0$ 时除数为 $0$,所以要特判,以及 $r$ 超过 $n$ 的情况。
代码(当然也是现场写的):
int ans = n * k;
for (int l = 1, r; l <= n; l = r + 1) { if (k / l) r = min (n, k / (k / l) );
else break;// k / l 已经等于 0 了,乘上 0 不会对答案产生任何的贡献。 ans -= (r - l + 1) * (l + r) / 2 * (k / l); }
形式二:
给定 $n$,$m$,求 $\sum\limits_{i=1}^{\min(n,m)} \lfloor\frac{n}{i}\rfloor\lfloor\frac{m}{i}\rfloor$
由于 $\lfloor\frac{n}{i}\rfloor$ 的取值只有 $2\sqrt{n}$ 种,所以两者相乘,多了 $2\sqrt{n}$ 个取值,也就 $4\sqrt{n}$ 种。
之前,我们的 $r$ 设为 $n / (n / l)$,现在我们设为 $\min(n/(n / l), m / (m / l))$,代码如下:
for (int l = 1, r; l <= min (n, m); l = r + 1) { r = min (n / (n / l), m / (m / l) ); ans += (r - l + 1) * (n / l) * (m / l); }
形式三:
求 $\sum\limits_{i=1}^n f(i)\cdot \lfloor\frac{n}{i}\rfloor$。
受形式一的启发,为 $f$ 函数预处理前缀和,处理答案的时候,还是分配律。
代码大家可以自己探究一下。
数论分块例题:
第一题:
$P3935$ $Calculating$:若 $x$ 分解质因数结果为 $x=p_1^{k_1}p_2^{k_2}\cdots p_n^{k_n}$,令$f(x)=(k_1+1)(k_2+1)\cdots (k_n+1)$,求 $\sum_{i=l}^rf(i)$ 对 $998\,244\,353$ 取模的结果。
思路:
首先容斥一下,只要求 $1$ ~ $r$ 的 $f$ 和然后减下 $1$ ~ $l-1$ 的就行。
先看 $(k_1+1)(k_2+1)\cdots (k_n+1)$,这个东西其实就是 $x$ 的因数个数。
粗略证明一下:每个 $k$ 次方我们可以选择 $0$~$k$ 次方乘到数 $t$ 上,
这样构造的数 $t$ 互不相同且一一对应 $x$ 的因数。
那么就成了 $\sum\limits_{i=1}^n d(i)$,$d(i)$ 表示 $i$ 的因数个数。
再来看怎么求这个,枚举因数 $k$,它在 $1$ ~ $n$ 中成为因数的个数就是 $\lfloor\frac{n}{k}\rfloor$。
$k$ 可以取任意的 $1$ ~ $n$ 的整数,于是就成了:
$\sum\limits_{i=1}^n \lfloor\frac{n}{i}\rfloor$,这不就是数论分块吗,$O(\sqrt{n})$ 解决了,别忘了最终答案要 $f(r)-f(l-1)$。
代码:
#include <iostream> const long long mod = 998244353; using namespace std; long long l, r, x, y; long long f (long long n) { long long ret = 0; l = 1; for (; l != n + 1; l = r + 1) { r = n / (n / l); ret = (ret + (r - l + 1) * (n / l) % mod) % mod; } return ret; } int main () { scanf ("%lld%lld", &x, &y); printf ("%d", ( ( (f (y) - f (x - 1) ) % mod + mod) % mod) ); return 0; }
第二题:
拓展题:$P2260$ 模积和,这个需要用 $1$ ~ $i$ 平方和公式,等差数列求和公式,和超级繁琐的数论分块。
想要钻研的同学们可以去做一下。
代码:
#include <iostream> const int mod = 19940417, inv6 = 3323403; using namespace std; long long x, y, l, r; long long f (long long n, long long m) {//求解 sum (i = 1 to n) i * 下取整 (m / i) 的值 long long ret = 0; l = 1; for (; l != n + 1; l = r + 1) { if (m / l) r = min (n, m / (m / l) ); else break; ret = (ret + (l + r) * (r - l + 1) / 2 % mod * (m / l) % mod) % mod; } return ret; } long long sum (long long n) {return n * (n + 1) % mod * (2 * n + 1) % mod * inv6 % mod;} long long fun (long long n, long long m) {//求解 sum (i = 1 to n) i ^ 2 * 下取整 (n / i) * 下取整 (m / i) 的值 long long ret = 0; l = 1; for (; l <= min (n, m); l = r + 1) { r = min (n / (n / l), m / (m / l) ); ret = (ret + (sum (r) - sum (l - 1) ) * (m / l) % mod * (n / l) % mod) % mod; } return ret; } int main () { cin >> x >> y; if (x > y) swap (x, y); cout << ( (x * x % mod - f (x, x) ) * (y * y % mod - f (y, y) ) % mod - (x * x % mod * y % mod - y * f (x, x) % mod - x * f (x, y) % mod + fun (x, y) ) % mod + mod) % mod; return 0; }
一些有用的定义:
数论函数:值域定义在正整数上的函数。
积性函数:对于任何两个正整数$p$,$q$,都满足 $\gcd(p,q)=1$ 且 $f(p) \cdot f(q) = f(p\cdot q)$ 的数论函数 $f(n)$。
完全积性函数:对于任何两个正整数 $p$,$q$,都满足 $f(p)\cdot f(q)=f(p\cdot q)$ 的数论函数 $f(n)$。
艾弗森括号:形如 $[P]$,其中 $P$ 是一个命题,若为真,则返回值为 $1$,否则返回 $0$。
常见的积性函数:
单位函数 $ϵ(n)=[n=1]$。
幂函数 $Id^k(n)=n^k$,$Id^1(n)$ 通常就记为 $Id(n)$。
常值函数 $1(n)=1$。
因数个数函数 $d(n)=\sum\limits_{d|n} 1$
因数 $k$ 次方和函数 $\sigma_k(n)=\sum\limits_{d|n} d^k$,$k=0$ 时为因数个数,$k=1$ 时为因数和。
欧拉函数 $φ(n)=\sum\limits_{i=1}^n [\gcd(i,n)=1]$
莫比乌斯函数 $\mu (n):$ 分三种情况:
$n=1$:$\mu (n)=1$
$n$ 含有平方因子:$\mu(n)=0$
否则为 $(-1)^k$,$k$ 为 $n$ 不同质因子个数。
如果一个函数是积性函数,那么可以对其线性筛。
这些现在大家可能觉得没什么用,待会儿就知道了。
狄利克雷卷积:
我们定义两个数论函数 $f,g$ 在 $n$ 的狄利克雷卷积为:
$(f\times g)(n)=\sum\limits_{d|n} f(d)\cdot g(\frac{n}{d})$
性质满足交换律,结合律,分配律。
简单反演:
反演:如果一些数论函数较难求得,但是可以求出它的因数个数,因数和等,可以用反演简化运算。
目前我知道的反演有两种:莫比乌斯反演,欧拉反演。
很多题目两种反演都可以用,下面我们先来介绍一下这两个的主要内容吧。
莫比乌斯反演:
$[n=1]=\sum\limits_{d|n} \mu(d)$,意思是一个数所有因数的 $\mu$ 和等于这个数是否为 $1$。
更直白的说:如果 $n$ 为 $1$,那么 $\sum\limits_{d|n} \mu(d) = 1$,否则为 $0$。
欧拉反演:
$n=\sum\limits_{d|n} φ(n)$,一个数等于这个数所有因数的 $φ$ 和,证明过程太长,大家请自行 BFS。
例题:
了解了两种反演后,我们来做几道例题。
第一题:
求 $\sum\limits_{i=1}^n\sum\limits_{j=1}^m \gcd(i,j)$ 模 $998244353$ 的结果,以下全部假设 $n\leq m$。
首先,暴力是 $n^2\log n$ 的,过不了,考虑使用反演。
T1欧拉反演做法:
原式 $=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|i,d|j} φ(d)$,
注意这里如果一个数既是 $i$ 的因数又是 $j$ 的因数,那么它就是 $\gcd(i,j)$ 的因数。
内层循环和 $d$ 无关,我们可以把 $d$ 弄出来枚举因数得到:
$\sum\limits_{d=1}^n\sum\limits_{i=1}^n\sum\limits_{j=1}^m [d|i,d|j] φ(d)$,这一步 $d$ 相当于枚举所有 $\gcd(i,j)$ 的因数。
$phi(d)$ 与内层循环无关,可以用分配律提出来得到:$\sum\limits_{d=1}^n φ(d)\sum\limits_{i=1}^n\sum\limits_{j=1}^m [d|i,d|j]$。
然后发现内两层循环就是求倍数个数,很容易求得,$d$ 确定时,$[d|i,d|j]$ 的个数就是 $\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor$。
所以原式进一步化为:$\sum\limits_{d=1}^n φ (d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor$,使用整除分块和杜教筛能做到 $n^{\frac{2}{3}}$,
当然,一般题目不会有这么大的数据范围,线性筛就够用了。
代码(内含线性筛 $φ$ 的解释):
#include <iostream> #define int long long using namespace std; const int mod = 998244353; int n, m, ans, cnt; bool prime[1000005]; int primes[300005], phi[1000005]; void init () { phi[1] = 1; for (int i = 2; i <= 1000000; i ++){ if (! prime[i]) { primes[++ cnt] = i; phi[i] = i - 1;//i 是质数,1 ~ i - 1 都和它互素 } for (int j = 1; j <= cnt && i * primes[j] <= 1000000; j ++) { prime[i * primes[j] ] = true; if (i % primes[j] == 0) { phi[i * primes[j] ] = phi[i] * primes[j];//i 是 primes[j] 的倍数,此时 phi[i * primes[j] ] = phi[i] * primes[j]。 break; } phi[i * primes[j] ] = phi[i] * (primes[j] - 1);//i 和 primes[j] 互素,根据积性函数定义。 //phi[i * primes[j] ] = phi[i] * phi[primes[j] ],即 phi[i] * (primes[j] - 1)。 } phi[i] = (phi[i] + phi[i - 1]) % mod;//预处理前缀和 + 取模。 } } signed main () { init (); cin >> n >> m; if (n > m) swap (n, m); for (int l = 1, r; l <= n; l = r + 1) {//整除分块。 r = min (n / (n / l), m / (m / l) ); ans = (ans + (phi[r] - phi[l - 1]) * (n / l) % mod * (m / l) % mod) % mod; } cout << ans; return 0; }
T1莫比乌斯反演做法:
$\sum\limits_{d=1}^n d \cdot \sum\limits_{i=1}^n\sum\limits_{j=1}^m [\gcd(i,j)==d]$
若 $\gcd(i,j)=d$,那么 $\gcd(i/d,j/d)=1$。
化为 $\sum\limits_{d=1}^n d\cdot \sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}[\gcd(i,j)==1]$
此时使用莫反:$\sum\limits_{d=1}^n d\cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}\sum\limits\sum\limits_{x|i,x|j} \mu(x)$
枚举 $x$ 把 $\mu(x)$ 提出得:$\sum\limits_{d=1}^n d\cdot\sum\limits_{x=1}^m \mu(x) \cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}[x|i,x|j]$
内两层循环也是求倍数个数,化简为 $\lfloor\frac{n}{xd}\rfloor\lfloor\frac{m}{xd}\rfloor$
原式化为:$\sum\limits_{d=1}^n d\cdot\sum\limits_{x=1}^{\lfloor\frac{m}{d}\rfloor} \mu(x) \cdot\lfloor\frac{n}{xd}\rfloor\lfloor\frac{m}{xd}\rfloor$,把 $x$ 换成 $T$ 美观一些:
$\sum\limits_{d=1}^n d\cdot\sum\limits_{T=1}^{\lfloor\frac{m}{d}\rfloor} \mu(T) \cdot\lfloor\frac{n}{Td}\rfloor\lfloor\frac{m}{Td}\rfloor$
线性筛 $\mu$ 然后调和级数 $O(n\log n)$ 可以求得。(默认 $n$,$m$ 同阶。枚举 $Td$ 可以转换成欧拉反演,$O(n)$ 求)
(后面我将不再详细介绍每一步反演的过程,仅仅选择重要的几步介绍。)
线性筛 $\mu$ 的代码:
#include <iostream> using namespace std; int cnt; int primes[300005], mu[1000005]; bool primes[1000005]; int main () { for (int i = 2; i <= 1000000; i ++) { if (!prime[i]) { primes[++ cnt] = i; mu[i] = -1;//仅有一个质因子,它本身。注意:1不是质数。 } for (int j = 1; j <= cnt && i * primes[j] <= 1000000; j ++) { prime[i * primes[j] ] = true; if (i % primes[j] == 0) { mu[i * primes[j] ] = 0;//含有平方因子 primes[j] * primes[j]。 break; } mu[i * primes[j] ] = -mu[i];//多了一个因子 primes[j],乘上 -1,或者根据积性函数的定义。 } } return 0; }
第二题:
$2.$ 求 $\sum\limits_{i=1}^n\sum\limits_{j=1}^m [\gcd(i,j)==1]$
这题貌似只能用莫比乌斯反演,大家可以先自己尝试一下,这个比较简单。
T2莫比乌斯反演做法:
$\sum\limits_{i=1}^n\sum\limits_{j=1}^m [\gcd(i,j)==1]$,以下设 $n<m$
$=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|i,d|j} \mu(d)$
$=\sum\limits_{d=1}^n\mu(d)\cdot \sum\limits_{i=1}^n\sum\limits_{j=1}^m [d|i,d|j]$
$=\sum\limits_{d=1}^n\mu(d)\cdot \lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor$
预处理 $\mu$ 前缀和 $O(n)$ 加整除分块单次 $\sqrt{n}$。
(可能大家觉得整除分块可以不用,因为时间复杂度瓶颈在线性筛。但是学了杜教筛之后,这题的数据范围就可以到 $10^{10}$ 卡线性筛)
第三题:
$3.$ 求 $\sum\limits_{i=1}^n\sum\limits_{j=1}^m f(\gcd(i,j) )$,其中 $f$ 是数论函数。
这题也不能用欧拉反演做,因为 $f$ 是个函数,并不知道因数个数,只能枚举 $\gcd$
T3莫比乌斯反演做法:
$\sum\limits_{i=1}^n\sum\limits_{j=1}^m f(\gcd(i,j) )$
$=\sum\limits_{d=1}^n f(d)\cdot\sum\limits_{i=1}^n\sum\limits_{j=1}^m [\gcd(i,j)==d]$
$=\sum\limits_{d=1}^n f(d)\cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}[\gcd(i,j)==1]$
$=\sum\limits_{d=1}^n f(d)\cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}\sum\limits_{x|i,x|j}\mu(x)$
$=\sum\limits_{d=1}^n f(d)\sum\limits_{x=1}^{\lfloor\frac{n}{d}\rfloor}\mu(x) \cdot\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}[x|i,x|j]$
$=\sum\limits_{d=1}^n f(d)\sum\limits_{x=1}^{\lfloor\frac{n}{d}\rfloor}\mu(x) \cdot\lfloor\frac{n}{dx}\rfloor\lfloor\frac{m}{dx}\rfloor$
枚举 $dx$,令其 $=T$ 得:
$=\sum\limits_{T=1}^n\sum\limits_{x|T} f(\frac{T}{x})\cdot \mu(x)\cdot\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor$
内层 $\sum$ 提出来。
$=\sum\limits_{T=1}^n \lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\sum\limits_{x|d}f(\frac{T}{x})\cdot \mu(x)\cdot$
然后发现是个狄利克雷卷积。
$=\sum\limits_{T=1}^n \lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor (f\cdot \mu) (T)$
预处理 $O(n)$ 加整除分块单次询问 $\sqrt{n}$。
第四题:
设 $d(x)$ 为 $x$ 的约数个数,给定 $n,m$,求 $\sum_{i=1}^n\sum_{j=1}^md(i\cdot j)$。
我会尽量写的详细些。
$\sum\limits_{i=1}^n\sum\limits_{j=1}^m d(i\cdot j)$($n < m$)
$=\sum\limits_{i=1}^n\sum\limits_{j=1}^m \sum\limits_{x|i}\sum\limits_{y|j} [\gcd(x,y)=1]$(特殊性质,证明看那题的题解)
$=\sum\limits_{i=1}^n\sum\limits_{j=1}^m \sum\limits_{x=1}^n\sum\limits_{y=1}^m[x|i,y|j,\gcd(x,y)=1]$
$=\sum\limits_{x=1}^n\sum\limits_{y=1}^m \sum\limits_{i=1}^n\sum\limits_{j=1}^m[x|i,y|j,\gcd(x,y)=1]$
$=\sum\limits_{x=1}^n\sum\limits_{y=1}^m \lfloor\frac{n}{x}\rfloor\lfloor\frac{m}{y}\rfloor[\gcd(x,y)=1]$
$=\sum\limits_{x=1}^n\sum\limits_{y=1}^m \lfloor\frac{n}{x}\rfloor\lfloor\frac{m}{y}\rfloor\sum\limits_{d|x,d|y}\mu(d)$
$=\sum\limits_{d=1}^n\sum\limits_{x=1}^n\sum\limits_{y=1}^m\lfloor\frac{n}{x}\rfloor\lfloor\frac{m}{y}\rfloor[d|x,d|y]\cdot \mu(d)$
$=\sum\limits_{d=1}^n\mu(d)\sum\limits_{x=1}^n\sum\limits_{y=1}^m\lfloor\frac{n}{x}\rfloor\lfloor\frac{m}{y}\rfloor[d|x,d|y]$
枚举 $x$ $y$,改为枚举 $x\cdot d$,$y\cdot d$。这个一定被 $d$ 整除,可以去掉这个棘手的条件了。
$=\sum\limits_{d=1}^n\mu(d)\sum\limits_{x=1}^{\lfloor\frac{n}{d}\rfloor}\sum\limits_{y=1}^{\lfloor\frac{m}{d}\rfloor}\lfloor\frac{n}{xd}\rfloor\lfloor\frac{m}{dy}\rfloor$
$=\sum\limits_{d=1}^n\mu(d)(\sum\limits_{x=1}^{\lfloor\frac{n}{d}\rfloor}\lfloor\frac{n}{xd}\rfloor\cdot\sum\limits_{y=1}^{\lfloor\frac{m}{d}\rfloor}\lfloor\frac{m}{dy}\rfloor)$
大家可能还没发现后面可以用整除分块,我们令 $n'=\lfloor\frac{n}{d}\rfloor$,$m'=\lfloor\frac{m}{d}\rfloor$。
这下一目了然,$=\sum\limits_{d=1}^n\mu(d)(\sum\limits_{x=1}^{n'} \lfloor\frac{n'}{x}\rfloor\cdot \sum\limits_{y=1}^{m'} \lfloor\frac{m'}{y}\rfloor)$。
注意这里 $\sum\limits_{x=1}^{n'} \lfloor\frac{n'}{x}\rfloor\cdot \sum\limits_{y=1}^{m'} \lfloor\frac{m'}{y}\rfloor$ 和 $\sum\limits_{x=1}^{n'} \lfloor\frac{n'}{x}\rfloor \sum\limits_{y=1}^{m'} \lfloor\frac{m'}{y}\rfloor$ 的区别:一个是两者相乘,另一个是 $\sum$ 套 $\sum$。
我们再来讲一下这个东西怎么整除分块:$n'=\lfloor\frac{n}{d}\rfloor$,$m'=\lfloor\frac{m}{d}\rfloor$,不难发现大量 $n'$,$m'$ 相同,内层还有一个整除分块。
这时有两个选择,两层整除分块:$n^{\frac{3}{4}}$
预处理 $n=1$ ~ $50000$ 时,$\sum\limits_{i=1}^n\lfloor\frac{n}{i}\rfloor$。
怎么预处理呢?我们发现 $\sum\limits_{i=1}^n\lfloor\frac{n}{i}\rfloor=\sum\limits_{i=1}^n d(i)$,这个在整除分块例题的时候证明过,线性筛 $d$ 函数就行了。
预处理 $\mu$,$d$ 函数的前缀和 $O(n)$ 再加上整除分块单次询问 $O(\sqrt{n})$,可以通过此题。
代码(内含线性筛 $d$ 函数的解释):
UPD on 2023/04/05:今天突然发现算内层整除分块时顺便记忆化也可以,还更方便,虽然是 $\sqrt{n}$ 的,但是比两层整除分块快些。
$O(n)$ 预处理 $+\sqrt{n}$ 单次询问代码:(??? 随便一写竟然跑到最优解第一页的末尾。)
#include <iostream> using namespace std; int T, n, m; int cnt; long long mu[50005], num[50005], sigma[50005], primes[20005];//num[i] 表示 i 最小质因子的数量,看到后面注释就能明白 bool prime[50005]; void init () { mu[1] = sigma[1] = 1; for (int i = 2; i <= 50000; i ++) { if (!prime[i]) { primes[++ cnt] = i; sigma[i] = 2;//素数有两个约数,它本身和 1 mu[i] = -1; num[i] = 1; } for (int j = 1; j <= cnt && i * primes[j] <= 50000; j ++) { prime[i * primes[j] ] = true; if (i % primes[j] == 0) { mu[i * primes[j] ] = 0;//有平方因子 sigma[i * primes[j] ] = sigma[i] / (num[i] + 1) * (num[i] + 2); /*设 i 被分解后各项的次方分别是:a_1,a_2,a_3...a_n。(底数从小到大排列的) 在整除分块例题中证明过 d[i] = (a_1 + 1) * (a_2 + 1) * ... * (a_n + 1) 现在多了一个最小质因数,d[i * primes[j] ] = (a_1 + 2) * (a_2 + 1) * ... * (a_n + 1) 所以我们需要记录 a_1,也就是最小质因子的数量。 */ num[i * primes[j] ] = num[i] + 1;//那么最小质因子的数量显然加上一 break; } mu[i * primes[j] ] = -mu[i]; sigma[i * primes[j] ] = sigma[i] * 2;//i 所有的因子乘上 primes[j] 可以构造出新的因子。 num[i * primes[j] ] = 1;//primes[j] 是 i * primes[j] 的最小质因数。 //而 i % primes[j] != 0,所以 num[i * primes[j] ] = 1 } sigma[i] += sigma[i - 1];//预处理前缀和 mu[i] += mu[i - 1]; } } int f (int x) {return sigma[x];}//求解 Σ下取整 (x/i),根据刚刚的推论,它就等于 sigma[1] +... + sigma[x] int main () { init (); scanf ("%d", &T); while (T --) { long long ans = 0; scanf ("%d%d", &n, &m); if (n > m) swap (n, m); for (int l = 1, r; l <= n; l = r + 1) {//整除分块 r = min (n / (n / l), m / (m / l) ); ans += long (mu[r] - mu[l - 1]) * f (n / l) * f (m / l); //这一段 n' m' 的值是一样的,可以把 mu 提出来用前缀和。 } printf ("%lld\n", ans); } return 0; }
记忆化代码:
#include <iostream> using namespace std; int T, n, m, cnt; int mem[50005]; long long primes[50005], mu[50005]; bool prime[50005]; void init () { mu[1] = 1; for (int i = 2; i <= 50000; i ++) { if (!prime[i]) { primes[++ cnt] = i; mu[i] = -1; } for (int j = 1; j <= cnt && i * primes[j] <= 50000; j ++) { prime[i * primes[j] ] = true; if (i % primes[j] == 0) break; mu[i * primes[j] ] = -mu[i]; } mu[i] += mu[i - 1]; } } long long f (int x) { if (mem[x]) return mem[x]; for (int l = 1, r; l <= x; l = r + 1) { r = x / (x / l); mem[x] += (r - l + 1) * (x / l); } return long (mem[x]); } int main () { init (); scanf ("%d", &T); long long ans; while (T --) { ans = 0; scanf ("%d%d", &n, &m); if (n > m) swap (n, m); for (int l = 1, r; l <= n; l = r + 1) { r = min (n / (n / l), m / (m / l) ); ans += long (mu[r] - mu[l - 1]) * f (n / l) * f(m / l); } printf ("%lld\n", ans); } return 0; }
总结:
反演时通常考虑枚举一个数,然后快速求出因数个数啥的;
如果不能继续反演,可以考虑枚举两个数相乘啥的,就能从绝境中走出。
反演时两种都试一下,选择最好写,时间复杂度合适的算法。
杜教筛:
杜教筛也是反演的基础,我们先来了解一下它吧。
介绍:
杜教筛三问:名字怎么来的?有什么用?时间复杂度如何?
$1.$ 由一位姓杜的学长初次在国内使用并传开,后引用他的名字命名这个算法。
$2.$ 可以在非线性时间内求解积性函数 $f$ 前 $n$ 项的和。
$3.$ 不加预处理,时间复杂度 $O(n^\frac{3}{4})$,加上预处理 $O(n^\frac{2}{3})$。
(大家可能觉得 $n^{\frac{1}{3}}$ 和 $O(n)$ 差距很小,事实上,在 $n=2^{31}$ 时,两者相差将近 $1300$ 倍!)
例题:
给定一个正整数,求:$ans_1=\sum_{i=1}^n φ(i)$,$ans_2=\sum_{i=1}^n \mu(i)$
我们一边讲题一边介绍杜教筛吧。
考虑构造数论函数使 $f\times g = h$,并且设我们要求的函数是 $f$ 的前缀和,尝试化简它。
$\sum\limits_{i=1}^n\sum\limits_{d|i} g(d)f(\frac{n}{d})= \sum\limits_{i=1}^n h(i)$
枚举 $d$ 得:$\sum\limits_{d=1}^n g(d)\sum\limits_{i=1}^n [d|i]f(\frac{i}{d})$
内层 $\sum$ 可以化简,枚举 $id$。$\sum\limits_{d=1}^n g(d)\sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor} f(i)$
所以 $\sum\limits_{d=1}^n g(d) \sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor} f(i)=\sum\limits_{i=1}^n h(i)$
然后把 $d=1$ 时拆开得到:$g(1)\sum\limits_{i=1}^n f(i) + \sum\limits_{d=2}^n g(d) \sum\limits_{i=1}^{\lfloor\frac{n}{d}\rfloor} f(i)=\sum\limits_{i=1}^n h(i)$
设 $s(i)=f(1)+f(2)+...+f(i)$
又化简为 $s(n)g(1) + \sum\limits_{d=2}^n g(d) s(\lfloor\frac{n}{d}\rfloor)=\sum\limits_{i=1}^n h(i)$
所以 $s(n)=\frac{\sum\limits_{i=1}^n h(i) - \sum\limits_{d=2}^n g(d) s(\lfloor\frac{n}{d}\rfloor)}{g(1)}$,这个就是杜教筛公式了。
后面可以整除分块,前面 $h$ 函数前缀和我们只要构造 $O(\sqrt{n})$ 以内可求前缀和的 $h$ 函数就行了(瓶颈在后面的 $\sqrt{n}$)。
加上记忆化,时间复杂度为 $n^\frac{3}{4}$,预处理 $k$ 以内的 $s$ 便可做到 $T(n)=O(k)+O(\frac{n}{\sqrt{k}})$,$k$ 取 $n^\frac{2}{3}$ 时最优,时间复杂度为 $n^\frac{2}{3}$。
求 $φ$ 前 $n$ 项和:
取 $g=1$ (常值函数 $1(n)=1$),因为 $f$ 是 $φ$ 函数。根据欧拉反演,$φ\times 1 = Id^1$,所以 $h=Id^1$,这些都很好求。
带回得到 $s(n)=\frac{\sum\limits_{i=1}^n i - \sum\limits_{d=2}^n (s(\lfloor\frac{n}{d}\rfloor)\cdot 1)}{1}$。
进一步化简得到:$s(n)=\frac{(n + 1)\cdot n}{2} - \sum\limits_{d=2}^n s(\lfloor\frac{n}{d}\rfloor)$。
代码:
int sum_phi (int n) {//求 s(n) 的值 if (n <= b) return s[n];//提前筛好的 if (map[n]) return map[n];//记忆化 int ans = n * (n + 1) / 2; for (int l = 2, r; l <= n; l = r + 1) {//整除分块 r = n / (n / l); ans -= sum_phi (n / l) * (r - l + 1); } return map[n] = ans;//记忆化 }
求 $\mu$ 前 $n$ 项和:
依然取 $g=1$,$f$ 当然取 $\mu$ 函数。根据莫比乌斯反演,$\mu \times 1 = ϵ$,所以 $h=ϵ$,也很好求。
化简为 $s(n)=1-\sum\limits_{d=2}^n s(\lfloor\frac{n}{d}\rfloor)$。
int sum_mu (int n) { if (n <= b) return s[n]; if (map[n]) return map[n]; int ans = 1; for (int l = 2, r; l <= n; l = r + 1) { r = n / (n / l); ans -= sum_phi (n / l) * (r - l + 1) / 2; } return map[n] = ans;//记忆化 }
例题:
恭喜你已经学完了大部分反演的内容,我们做几道例题。
原文链接:https://www.cnblogs.com/Xy-top/p/17277405.html
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:莫比乌斯反演,欧拉反演学习笔记 - Python技术站

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫 