1. 激活函数
Rectified Linear Unit(ReLU) - 用于隐层神经元输出
Sigmoid - 用于隐层神经元输出
Softmax - 用于多分类神经网络输出
Linear - 用于回归神经网络输出(或二分类问题)
ReLU函数计算如下:

Sigmoid函数计算如下:
Softmax函数计算如下:
Softmax激活函数只用于多于一个输出的神经元,它保证所以的输出神经元之和为1.0,所以一般输出的是小于1的概率值,可以很直观地比较各输出值。
2. 为什么选择ReLU?
深度学习中,我们一般使用ReLU作为中间隐层神经元的激活函数,AlexNet中提出用ReLU来替代传统的激活函数是深度学习的一大进步。我们知道,sigmoid函数的图像如下:

而一般我们优化参数时会用到误差反向传播算法,即要对激活函数求导,得到sigmoid函数的瞬时变化率, 其导数表达式为:

对应的图形如下:

由图可知,导数从0开始很快就又趋近于0了,易造成“梯度消失”现象,而ReLU的导数就不存在这样的问题,它的导数表达式如下:

Relu函数的形状如下(蓝色):

对比sigmoid类函数主要变化是:1)单侧抑制 2)相对宽阔的兴奋边界 3)稀疏激活性。这与人的神经皮层的工作原理接近。
leak_relu的函数表达式是:

其中a是一个负的斜率,默认为0.01.
leak_relu函数的进一步说明:
**计算Leaky ReLU激活函数
tf.nn.leaky_relu(
features,
alpha=0.2,
name=None )
参数: features:一个Tensor,表示预激活
alpha:x<0时激活函数的斜率
ame:操作的名称(可选)
返回值:激活值
**
非饱和激活函数:Leaky ReLU的图像
数学表达式: y = max(0, x) + leak*min(0,x)
优点:
1.能解决深度神经网络(层数非常多)的“梯度消失”问题,浅层神经网络(三五层那种)才用sigmoid 作为激活函数。
2.它能加快收敛速度。
————————————————
版权声明:本文为CSDN博主「qq_41621342」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_41621342/article/details/105262875
relu函数的进步一说明:
https://blog.csdn.net/qq_23304241/article/details/80300149
3. 为什么需要偏移常量?
通常,要将输入的参数通过神经元后映射到一个新的空间中,我们需要对其进行加权和偏移处理后再激活,而不仅仅是上面讨论激活函数那样,仅对输入本身进行激活操作。比如sigmoid激活神经网络的表达式如下:

x是输入量,w是权重,b是偏移量(bias)。这里,之所以会讨论sigmoid函数是因为它能够很好地说明偏移量的作用。
权重w使得sigmoid函数可以调整其倾斜程度,下面这幅图是当权重变化时,sigmoid函数图形的变化情况:

上面的曲线是由下面这几组参数产生的:

我们没有使用偏移量b(b=0),从图中可以看出,无论权重如何变化,曲线都要经过(0,0.5)点,但实际情况下,我们可能需要在x接近0时,函数结果为其他值。下面我们改变偏移量b,它不会改变曲线大体形状,但是改变了数值结果:

上面几个sigmoid曲线对应的参数组为:

这里,我们规定权重为1,而偏移量是变化的,可以看出它们向左或者向右移动了,但又在左下和右上部位趋于一致。
当我们改变权重w和偏移量b时,可以为神经元构造多种输出可能性,这还仅仅是一个神经元,在神经网络中,千千万万个神经元结合就能产生复杂的输出模式。
————————————————
版权声明:本文为CSDN博主「Leo_Xu06」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/Leo_Xu06/article/details/53708647
=============================分割线=======================================
2021.11.17(https://www.jianshu.com/p/78ae6dbfd20f)
2.1 定义
在数学,尤其是概率论和相关领域中,Softmax函数,或称归一化指数函数
,是逻辑函数的一种推广。它能将一个含任意实数的K维的向量z的“压缩”到另一个K维实向量σ(z) 中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。
2.2公式

在多项逻辑回归和线性判别分析中,函数的输入是从K个不同的线性函数得到的结果,而样本向量 x 属于第 j 个分类的概率为:

这可以被视作K个线性函数x→xTw1,...,→xTwKSoftmax函数的复合(xTwxw)
2.3 python实现
import numpy as np def softmax(x): orig_shape=x.shape if len(x.shape)>1: #Matrix #shift max whithin each row constant_shift=np.max(x,axis=1).reshape(1,-1) x-=constant_shift x=np.exp(x) normlize=np.sum(x,axis=1).reshape(1,-1) x/=normlize else: #vector constant_shift=np.max(x) x-=constant_shift x=np.exp(x) normlize=np.sum(x) x/=normlize assert x.shape==orig_shape return x
2.4 函数图像
def softmax(x): orig_shape=x.shape if len(x.shape)>1: #Matrix #shift max whithin each row constant_shift=np.max(x,axis=1).reshape(1,-1) x-=constant_shift x=np.exp(x) normlize=np.sum(x,axis=1).reshape(1,-1) x/=normlize else: #vector constant_shift=np.max(x) x-=constant_shift x=np.exp(x) normlize=np.sum(x) x/=normlize assert x.shape==orig_shape return x softmax_inputs = np.arange(-10,10) softmax_outputs=softmax(softmax_inputs) print("Sigmoid Function Input :: {}".format(softmax_inputs)) print("Sigmoid Function Output :: {}".format(softmax_outputs)) # 画图像 plt.plot(softmax_inputs,softmax_outputs) plt.xlabel("Softmax Inputs") plt.ylabel("Softmax Outputs") plt.show()

这几天学习了一下softmax激活函数,以及它的梯度求导过程,整理一下便于分享和交流!
一、softmax函数
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类!
假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个元素的softmax值就是
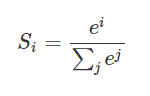
更形象的如下图表示:

softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用,就映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们就可以将它理解成概率,在最后选取输出结点的时候,我们就可以选取概率最大(也就是值对应最大的)结点,作为我们的预测目标!
为什么要引入激活函数
如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下你每一层输出都是上层输入的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,这种情况就是最原始的感知机(Perceptron)了。
正因为上面的原因,我们决定引入非线性函数作为激励函数,这样深层神经网络就有意义了(不再是输入的线性组合,可以逼近任意函数)。最早的想法是sigmoid函数或者tanh函数,输出有界,很容易充当下一层输入(以及一些人的生物解释balabala)。激活函数的作用是为了增加神经网络模型的非线性。否则你想想,没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。所以你没有非线性结构的话,根本就算不上什么神经网络。
tanh的绘制
tanh是双曲函数中的一个,tanh()为双曲正切。在数学中,双曲正切“tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。
公式

其实tanh(x)=2*sigmoid(2*x)-1
特点
- 函数:y=tanh x;
- 定义域:R
- 值域:(-1,1)。
- y=tanh x是一个奇函数,其函数图像为过原点并且穿越Ⅰ、Ⅲ象限的严格单调递增曲线,其图像被限制在两水平渐近线y=1和y=-1之间。
图像

python绘制tanh函数
import math
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
fig = plt.figure(figsize=(6, 4))
ax = fig.add_subplot(111)
x = np.linspace(-10, 10)
y = tanh(x)
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.set_xticks([-10, -5, 0, 5, 10])
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0))
ax.set_yticks([-1, -0.5, 0.5, 1])
plt.plot(x, y, label="Sigmoid", color="red")
plt.legend()
plt.show()结果:

作者:致Great
链接:https://www.jianshu.com/p/7409c8f1cdca
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
==============================分割线========================================
另外,可以参考的讲解:
https://zhuanlan.zhihu.com/p/22142013
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:深度学习常用激活函数之 Sigmoid & ReLU & Softmax & tanh - Python技术站

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫 