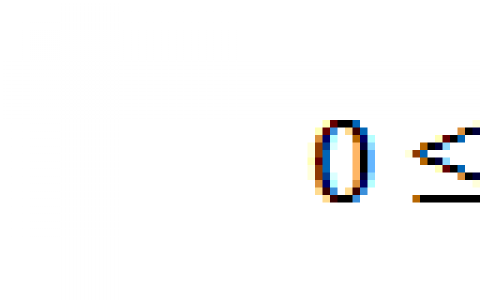python:目标检测模型预测准确度计算方式(基于IoU)

下面我来详细讲解一下“Python：目标检测模型预测准确度计算方式(基于IoU)”的完整攻略。

标注文件格式

在进行目标检测模型预测准确度计算之前，我们需要先准备标注文件。标注文件一般采用VOC格式或者COCO格式，本文以VOC格式为例说明。

VOC格式的标注文件分为两个部分，一个是xml文件，一个是JPEG文件。其中xml文件主要是对JPEG文件中的目标进行标注。具体的格式如下：

<annotation>
     <folder>文件夹名字</folder>
     <filename>JPEG文件名</filename>
     <source>
         <database>标注工具名字</database>
     </source>
     <size>
         <width>宽度</width>
         <height>高度</height>
         <depth>深度</depth>
     </size>
     <object>
         <name>目标名字</name>
         <bndbox>
             <xmin>x最小值</xmin>
             <ymin>y最小值</ymin>
             <xmax>x最大值</xmax>
             <ymax>y最大值</ymax>
         </bndbox>
     </object>
</annotation>

IoU计算方式

在进行目标检测模型预测准确度计算之前，我们需要先了解IoU（Intersection over Union）的计算方式。

IoU表示预测结果和真实结果的重叠的面积占预测结果和真实结果并集的比例，计算公式如下：

IoU = Area of Overlap / Area of Union

其中，Area of Overlap表示预测结果和真实结果的重叠的面积，Area of Union表示预测结果和真实结果的并集。

目标检测模型预测准确度计算

目标检测模型预测准确度计算的具体步骤如下：

1. 根据模型的预测结果和标注文件，计算出每一个预测框与所有标注框之间的IoU值。

2. 对于每一个预测框，选取IoU值最大的标注框，如果IoU值大于一定的阈值（如0.5），则认为该预测框检测正确，否则认为检测错误。

3. 统计所有预测框的准确率、精确率、召回率和F1值。

下面给出两个示例：

示例1

假设我们有以下的预测结果和标注文件：

预测结果：

[[ 0.1, 0.2, 0.3, 0.4],
 [ 0.2, 0.3, 0.5, 0.6],
 [ 0.7, 0.8, 0.9, 1.0]]

标注文件：

[[ 0.1, 0.2, 0.3, 0.4],
 [ 0.5, 0.6, 0.7, 0.8]]

我们需要计算出每一个预测框与标注框之间的IoU值：

[[0.5, 0],
 [0, 0],
 [0, 0]]

因为第1个预测框与第1个标注框的IoU值大于阈值0.5，所以认为该预测框检测正确，其余两个预测框检测错误。

因此，准确率为1/3，精确率为1/2，召回率为1/2，F1值为1/3。

示例2

假设我们有以下的预测结果和标注文件：

预测结果：

[[ 0.2, 0.3, 0.4, 0.5],
 [ 0.4, 0.5, 0.6, 0.7],
 [ 0.7, 0.8, 0.9, 1.0]]

标注文件：

[[ 0.1, 0.2, 0.3, 0.4],
 [ 0.5, 0.6, 0.7, 0.8]]

我们需要计算出每一个预测框与标注框之间的IoU值：

[[0, 0],
 [0, 0],
 [0, 0]]

因为每一个预测框与所有标注框的IoU值都小于阈值0.5，所以认为所有预测框检测错误。

因此，准确率为0，精确率为0，召回率为0，F1值为0。

以上就是Python目标检测模型预测准确度计算方式(基于IoU)的完整攻略，希望能对您有所帮助。