深度学习（十一） 残差网络

前言

我们都知道增加网络的宽度和深度可以很好的提高网络的性能，深的网络一般都比浅的的网络效果好，比如说一个深的网络A和一个浅的网络B，那A的性能至少都能跟B一样，为什么呢？因为就算我们把A的网络参数全部迁移到B的前面几层，而B后面的层只是做一个等价的映射，就达到了A网络的一样的效果。一个比较好的例子就是VGG，该网络就是在AlexNex的基础上通过增加网络深度大幅度提高了网络性能。

 

 

但事实真的是这样的吗？不然，通过实验我们发现，当网络层数达到一定的数目以后，网络的性能就会饱和，再增加网络的性能就会开始退化，但是这种退化并不是由过拟合引起的，因为我们发现训练精度和测试精度都在下降，这说明当网络变得很深以后，深度网络就变得难以训练了。

 

介绍

ResNet的出现其实就是为了解决网络深度变深以后的性能退化问题。

 

 

ResNet就是用这种跳跃结构来作为网络的基本结构。为什么要使用这种结构呢？作者认为，本来我们要优化的目标是H(x)=F(x)+x（x就是该结构的输入）但是通过这种结构以后就把优化的目标由H(x)转化为H(x)-x。 

那么问题又来了，优化目标转化后又有什么用呢，为什么可以通过这种方式来解决退化问题呢？我们之前说到，深网络在浅网络的基础上只要上面几层做一个等价映射就可以达到浅网络同样的效果，但是为什么不行呢，就是因为我们的算法很难将其训练到那个程度，也就是说没办法将上面几层训练到一个等价映射，以至于深网络最后达到了一个更差的效果。那么这时，我们把训练目标转变，由原来的H(x)转为H(x)-x(残差网络本质)，因为这时候就不是把上面几层训练到一个等价映射了，而是将其逼近与0（resnet学习的是残差函数F(x) = H(x) - x, 这里如果F(x) = 0, 那么就是上面提到的恒等映射），这样训练的难度比训练到一个等价映射应该下降了很多。 

也就是说，在一个网络中（假设有5层），如果前面四层已经达到一个最优的函数，那第五层就是没有必要的了，这时我们通过这种跳跃结构，我们的优化目标就从一个等价映射变为逼近0了，逼近其他任何函数都会造成网络退化。通过这种方式就可以解决网络太深难训练的问题。

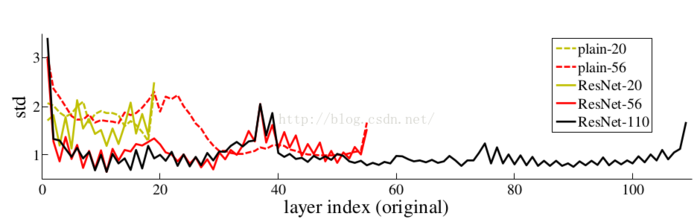
事实上，resnet是“shortcut connections”的在connections是在恒等映射下的特殊情况，它没有引入额外的参数和计算复杂度。 假如优化目标函数是逼近一个恒等映射, 而不是0映射， 那么学习找到对恒等映射的扰动会比重新学习一个映射函数要容易。从下图可以看出，残差函数一般会有较小的响应波动，表明恒等映射是一个合理的预处理。

 

实现

残差块的结构如下图：

它有二层，如下表达式，其中σ代表非线性函数ReLU

 

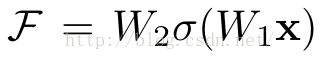
然后通过一个shortcut，和第2个ReLU，获得输出y

当需要对输入和输出维数进行变化时（如改变通道数目），可以在shortcut时对x做一个线性变换Ws，如下式，然而实验证明x已经足够了，不需要再搞个维度变换，除非需求是某个特定维度的输出，如文章开头的resnet网络结构图中的虚线，是将通道数翻倍。

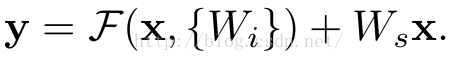
实验证明，这个残差块往往需要两层以上，单单一层的残差块(y=W1x+x)并不能起到提升作用。

 

残差网络的确解决了退化的问题，在训练集和校验集上，都证明了的更深的网络错误率越小，如下图

 

实际中，考虑计算的成本，对残差块做了计算优化，即将两个3x3的卷积层替换为1x1 + 3x3 + 1x1, 如下图。新结构中的中间3x3的卷积层首先在一个降维1x1卷积层下减少了计算，然后在另一个1x1的卷积层下做了还原，既保持了精度又减少了计算量。