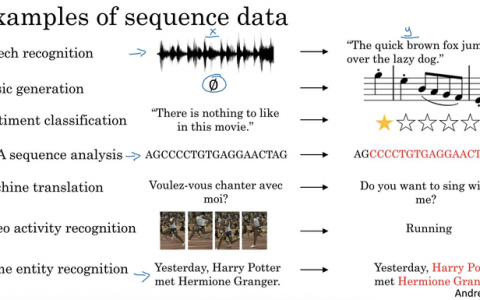
多项式回归，采用升维的方式，把x的幂当作新的特征，再利用线性回归方法解决

import numpy as np 
import matplotlib.pyplot as plt
​
x = np.random.uniform(-4,4,100)
y = 0.6*x**2 + x + 2 + np.random.normal(size=100)
​
# 单线性回归
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
y_predict = lin_reg.predict(X)
​
＃　多线性回归
X2 = np.hstack([X,X**2])
lin_reg = LinearRegression()
lin_reg.fit(X2,y)
y_predict2 = lin_reg.predict(X2)
​
plt.scatter(X,y)
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color='r')
plt.show()
​
lin_reg.coef_   # array([0.98046078, 0.59747765])
lin_reg.intercept_  # 2.0771588970176973

Scikit-learn中实现

from sklearn.preprocessing import PolynomialFeatures
​
poly = PolynomialFeatures(degree=2) # degree表示设置的最高幂的次数
X2 = poly.fit_transform(X)
X2.shape　   # (100, 3)
​
lin_reg = LinearRegression()
lin_reg.fit(X2,y)
y_predict2 = lin_reg.predict(X2)
​
plt.scatter(X,y)
plt.plot(np.sort(x),y_predict2[np.argsort(x)],color='r')
plt.show()
​
lin_reg.coef_   # array([0. ,0.98046078, 0.59747765])
lin_reg.intercept_  # 2.0771588970176964

Pipeline实现

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
​
pipeline = Pipeline([
    ('poly',PolynomialFeatures(degree=2)),
    ('std_scaler',StandardScaler()),
    ('lin_reg',LinearRegression())
])
X3 = pipeline.fit(X,y)
y_predict3 = pipeline.predict(X)
​
# pipeline.coef_ # 该项报错！ 放入管道后，不能直接取系数？？？

过拟合和欠拟合

机器学习算法之多项式回归

机器学习算法之多项式回归

def plot_learning_curve(algo, X_train, X_test, y_train, y_test):
    train_score = []
    test_score = []
    for i in range(1, len(X_train)+1):
        algo.fit(X_train[:i], y_train[:i])
    
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))
        
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(train_score), label="train")
    plt.plot([i for i in range(1, len(X_train)+1)], 
                               np.sqrt(test_score), label="test")
    plt.legend()
    plt.axis([0, len(X_train)+1, 0, 4])
    plt.show()
    
plot_learning_curve(LinearRegression(), X_train, X_test, y_train, y_test)
​
poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg, X_train, X_test, y_train, y_test)

交叉验证

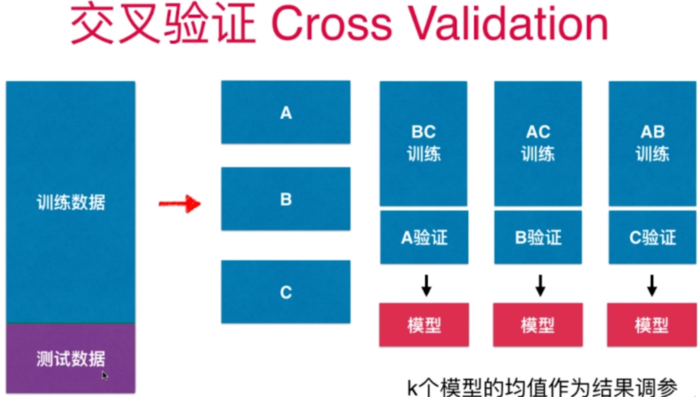
机器学习算法之多项式回归

 

机器学习算法之多项式回归

默认分成3份,要自定义,则修改参数 cv

cross_val_score(estimator,X_train,y_train) 结果返回３组（默认cv=3）的评分

import numpy as np
from sklearn import datasets
digits = datasets.load_digits()
X,y = digits.data,digits.target
from sklearn.model_selection import train_test_split
​
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)
​
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
​
knn_clf = KNeighborsClassifier()
cross_val_score(knn_clf,X_train,y_train)
# array([0.98895028, 0.97777778, 0.96629213])
​
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        # knn_clf.fit(X_train, y_train)
        # score = knn_clf.score(X_test, y_test)
        scores = cross_val_score(knn_clf,X_train,y_train,cv=3)
        score = np.mean(scores)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
            
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)
'''
Best K = 2
Best P = 2
Best Score = 0.9823599874006478
'''
best_knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=2, p=2)
best_knn_clf.fit(X_train,y_train)
# y_predict = best_knn_clf.predict(X_test)
best_knn_clf.score(X_test,y_test) # 0.980528511821975

回顾网格搜索

from sklearn.model_selection import GridSearchCV
​
grid_params = {
    'weights': ['distance'],
    'n_neighbors': [i for i in range(2, 11)], 
    'p': [i for i in range(1, 6)]
}
knn2_clf = KNeighborsClassifier()
clf = GridSearchCV(knn2_clf,grid_params,cv=3,n_jobs=-1)
clf.fit(X_train,y_train)
clf.best_score_ # 0.9823747680890538
clf.best_params_ # {'n_neighbors': 2, 'p': 2, 'weights': 'distance'}
clf.best_estimator_ 
# KNeighborsClassifier(n_neighbors=2, p=2,weights='distance')

偏差和方差

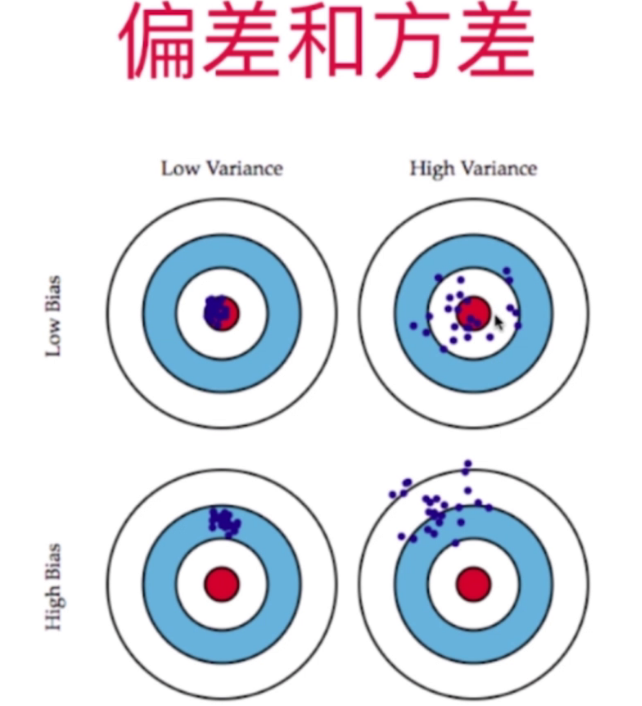
机器学习算法之多项式回归

 

机器学习算法之多项式回归偏差和方差通常是矛盾的.

减低偏差,会提高方差.

减低方差,会提高偏差.

有些算法天生是高方差的算法,如kNN.

非参数学习通常都是高方差算法,因为不对数据进行任何假设.

有些算法天生是高偏差的算法,如线性回归.

参数学习通常都是高偏差算法,因为对数据具有及强的假设.

 

机器学习算法,通常要解决的是高方差问题,比如过拟合,通常手段:

  1. 降低模型复杂度

  2. 减少数据维度;降噪

  3. 增加样本数

  4. 使用验证集

  5. 模型正则化

模型正则化--岭回归

机器学习算法之多项式回归

参数--alpha

import numpy as np
import matplotlib.pyplot as plt
​
# 构建数据集
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()
​
# 创建管道－－多项式线性回归
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
​
def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
​
# 切割数据集为训练和测试集
from sklearn.model_selection import train_test_split
​
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
​
# fit训练数据集，predict测试数据集，求取均方误差MSE
from sklearn.metrics import mean_squared_error
​
poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)
​
y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_poly_predict) # 167.94010867293571
# 绘制拟合函数曲线图
def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)
    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()
​
plot_model(poly_reg)
​
# 使用岭回归
from sklearn.linear_model import Ridge
​
def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha=alpha))
    ])
​
ridge1_reg = RidgeRegression(20, 0.0001)  # 1.3233492754051845  崎岖的线条
# ridge1_reg = RidgeRegression(20, 1)  # 1.1888759304218448 崎岖的光滑曲线
# ridge1_reg = RidgeRegression(20, 100)  # 1.3196456113086197   光滑的曲线
# ridge1_reg = RidgeRegression(20, 10000) #  1.8408455590998372 和x轴平行的直线
# 解析：　当alpha无穷大时，theta(i,i>=1)的平方必须都趋于０，当theta(i)都等于０时，即y=theta(0),和x轴平行
ridge1_reg.fit(X_train, y_train)
​
y1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict) # 1.3233492754051845
plot_model(ridge1_reg)

模型正则化--LASSO回归

机器学习算法之多项式回归

 lasso回归和岭回归比较

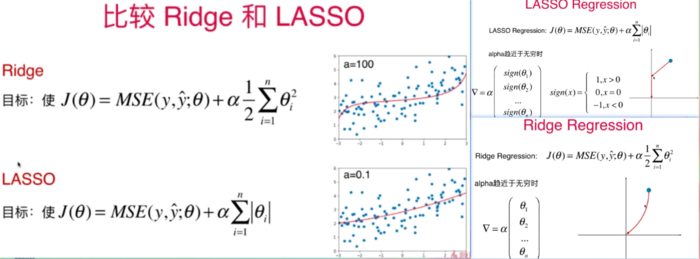
机器学习算法之多项式回归

机器学习算法之多项式回归

# 创建lasso管道
from sklearn.linear_model import Lasso
def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])
lasso1_reg = LassoRegression(20, 0.01) # 1.1496080843259966
# lasso1_reg = LassoRegression(20, 0.1) # 1.1213911351818648
# lasso1_reg = LassoRegression(20, 1) # 1.8408939659515595
lasso1_reg.fit(X_train, y_train)
​
y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
​
plot_model(lasso1_reg)

模型泛化--更具普遍性

我们训练机器学习的模型,不是为了在我们的训练集上有很好的测试结果,而是为了应对未来,在未知的数据集下有更好的预测结果.

L1&L2&弹性网络

机器学习算法之多项式回归

 

 

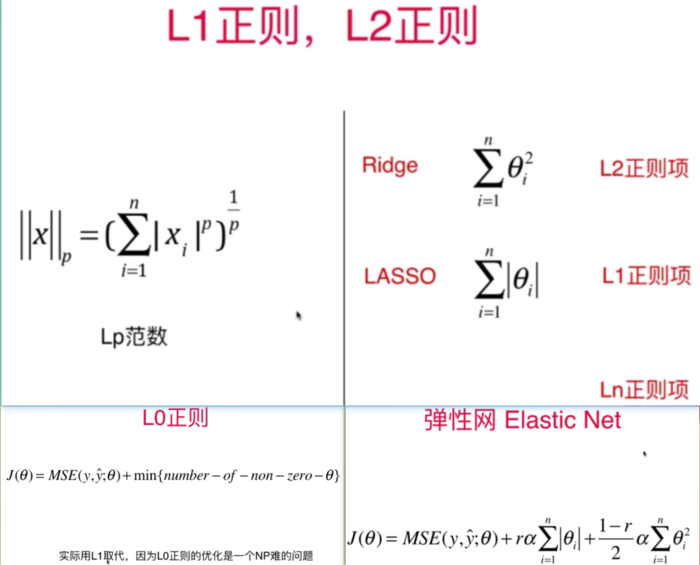
注: 上述笔记是自己在 慕课网学习 刘宇波老师<Python3入门机器学习 经典算法与应用https://s.imooc.com/Sk8Yr5g