一维离散卷积的运算是一种主要基于向量的计算方式
一.一维离散卷积的计算原理
一维离散卷积通常有三种卷积类型:full卷积,same卷积和valid卷积
1.full卷积
full卷积的计算过程如下:K沿着I顺序移动,每移动一个固定位置,对应位置的值相乘,然后对其求和
其中K称为卷积核或者滤波器或者卷积掩码
2.valid卷积
从full卷积的计算过程可知,如果K靠近I,就会有部分延伸到I之外,valid卷积只考虑能完全覆盖K内的情况,即K在I内部移动的情况
3.same卷积
首先在卷积核K上指定一个锚点,然后将锚点顺序移动到输入张量I的每一个位置处,对应位置相乘然后求和,卷积核锚点的位置一般有以下规则,假设卷积核的长度为FL:
如果FL为奇数,则锚点的位置在(FL-1)/2处
如果FL为偶数,则锚点的位置在(FL-2)/2处
4.full,same,valid卷积的关系
假设一个长度为L的一维张量与一个长度为FL的卷积核卷积,其中Fa代表计算same卷积时,锚点的位置索引,则两者的full卷积与same卷积的关系如下:
Csame=Cfull[FL-Fa-1,FL-Fa+L-2]
full卷积C与valid卷积C的关系如下:
C=C[FL-1,L-1]
same卷积C与valid卷积C的关系如下:
C=C[FL-Fa-2,L-Fa_2]
注意:大部分书籍中对卷积运算的定义分为两步。第1步是将卷积核翻转180;第2步是将翻转的结果沿输入张量顺序移动,每移动到一个固定位置,对应位置相乘然后求和,如Numpy中实现的卷积函数convolve和Scipy中实现的卷积函数convolve,函数内部都进行了以上两步运算。可见,最本质的卷积运算还是在第2步。Tensorflow中实现的卷积函数
tf.nn.conv1d(value,filters,stride,padding,use_cudnn_on_gpu=None,data_format=None,name=None)
其内部就没有进行第1步操作,而是直接进行了第2步操作
import tensorflow as tf
# 输入张量I
I=tf.constant(
[
[[3],[4],[1],[5],[6]]
]
,tf.float32
)
# 卷积核
K=tf.constant(
[
[[-1]],
[[-2]],
[[2]],
[[1]]
]
,tf.float32
)
I_conv1d_K=tf.nn.conv1d(I,K,1,'SAME')
session=tf.Session()
print(session.run(I_conv1d_K))
[[[ 3.]
[ -4.]
[ 10.]
[ 1.]
[-17.]]]
函数tf.nn.conv1d只实现了same卷积和valid卷积,它就是为更方便地搭建卷积神经网络而设计的。利用Numpy或者Scipy中的卷积函数convolve实现上述示例的full卷积代码如下:
import numpy as np
from scipy import signal
I=np.array([3,4,1,5,6],np.float32)
K=np.array([-1,-2,2,1],np.float32)
# 卷积核K翻转180
K_reverse=np.flip(K,0)
# r=np.convolve(I,K_reverse,mode='full')
r=signal.convolve(I,K_reverse,mode='full')
print(r)
[ 3. 10. 3. -4. 10. 1. -17. -6.]
注意:如果卷积核的长度是偶数,函数convolve和tf.nn.conv1d在实现same卷积时,其结果会略有不同,但也只是在边界处(两端)的值有所不同,这是因为这两个函数对卷积核锚点的位置定义不同,本质上就是从full卷积结果中取的区域不一样
二.一维卷积定理
1.一维离散傅里叶变换
Tensorflow通过函数fft和ifft分别实现一维离散的傅里叶变换及逆变换
import tensorflow as tf
# 输入长度为3的一维张量
f=tf.constant([4,5,6],tf.complex64)
session=tf.Session()
# 一维傅里叶变换
F=tf.fft(f)
print("傅里叶变换F的值:")
print(session.run(F))
# 计算F的傅里叶逆变换(显然与输入的f是相等的)
F_ifft=tf.ifft(F)
print("打印F的傅里叶逆变换的值:")
print(session.run(F_ifft))
傅里叶变换F的值:
[15. -5.9604645e-08j -1.4999998+8.6602545e-01j
-1.4999999-8.6602563e-01j]
打印F的傅里叶逆变换的值:
[4.+3.9736431e-08j 5.-3.1789145e-07j 6.+0.0000000e+00j]
2.卷积定理
假设有长度为L的一维张量I,I(l)代表I的第l个数,其中0≤l<L,有长度为FL的一维卷积核K,那么I与K的full卷积结果的尺寸为L+FL-1
首先,在I的末尾补零,将I的尺寸扩充到与full卷积尺寸相同,即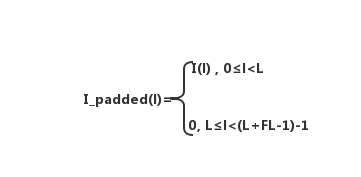
然后,将卷积核K翻转180得到K_rotate180,在末尾进行补零操作,且将K_rotate180的尺寸扩充到和full卷积相同,即
假设fft_Ip和fft_Krp分别是I_padded和K_rotate180_padded的傅里叶变换,那么I☆K的傅里叶变换等于fft_Ipfft_Krp,即
其中代表对应元素相乘,即对应位置的两个复数相乘,该关系通常称为卷积定理
从卷积定理中可以看出分别有对张量的补零操作(或称为边界扩充)和翻转操作。这两种操作在Tensorflow中有对应的函数实现,我们先介绍实现边界扩充的函数:
pad(tensor,padding,mode='CONSTANT',name=None,constant_value=0)
以长度为2的一维张量为例,上侧补1个0,下侧补2个0
import tensorflow as tf
x=tf.constant([2,1],tf.float32)
r=tf.pad(x,[[1,2]],mode='CONSTANT')
session=tf.Session()
print(session.run(r))
[0. 2. 1. 0. 0.]
当使用常数进行扩充时,也可以选择其他常数,通过参数constant_value进行设置,默认缺省值为0
import tensorflow as tf
x=tf.constant(
[
[1,2,3],
[4,5,6]
]
,tf.float32
)
# 常数边界扩充,上侧补1行10,下侧补2行10,右侧补1列10
r=tf.pad(x,[[1,2],[0,1]],mode='CONSTANT',constant_values=10)
session=tf.Session()
print(session.run(r))
[[10. 10. 10. 10.]
[ 1. 2. 3. 10.]
[ 4. 5. 6. 10.]
[10. 10. 10. 10.]
[10. 10. 10. 10.]]
除了常数边界扩充,还有其他扩充方式,可以通过参数mode设置,当mode='SYMMETRIC’时,代表镜像方式的边界扩充;当mode='REFLECT’时,代表反射方式的边界扩充,可以修改以上程序观察打印结果
Tensorflow通过函数reverse(tensor,axis,name=None)实现张量的翻转,二维张量的每一列翻转(沿"0"方向),则称为水平镜像;对每一行翻转(沿"1"方向),则称为垂直镜像
import tensorflow as tf
t=tf.constant(
[
[1,2,3],
[4,5,6]
]
,tf.float32
)
# 水平镜像
rh=tf.reverse(t,axis=[0])
# 垂直镜像
rv=tf.reverse(t,axis=[1])
# 逆时针翻转180:先水平镜像在垂直镜像(或者先垂直再水平)
r=tf.reverse(t,[0,1])
session=tf.Session()
print("水平镜像的结果:")
print(session.run(rh))
print("垂直镜像的结果:")
print(session.run(rv))
print("逆时针翻转180的结果:")
print(session.run(r))
水平镜像的结果:
[[4. 5. 6.]
[1. 2. 3.]]
垂直镜像的结果:
[[3. 2. 1.]
[6. 5. 4.]]
逆时针翻转180的结果:
[[6. 5. 4.]
[3. 2. 1.]]
掌握了张量边界扩充和翻转的对应函数后,利用卷积定理计算前面中x和K的full卷积
import tensorflow as tf
# 长度为5的输入张量
I=tf.constant(
[3,4,1,5,6],tf.complex64
)
# 长度为4的卷积核
K=tf.constant(
[-1,-2,2,1],tf.complex64
)
# 补0操作
I_padded=tf.pad(I,[[0,3]])
# 将卷积核翻转180
K_rotate180=tf.reverse(K,axis=[0])
# 翻转进行0操作
K_rotate180_padded=tf.pad(K_rotate180,[[0,4]])
# 傅里叶变换
I_padded_fft=tf.fft(I_padded)
# 傅里叶变换
K_rotate180_padded_fft=tf.fft(K_rotate180_padded)
# 将以上两个傅里叶变换点乘操作
IK_fft=tf.multiply(I_padded_fft,K_rotate180_padded_fft)
# 傅里叶逆变换
IK=tf.ifft(IK_fft)
# 因为输入的张量和卷积核都是实数,对以上傅里叶逆变换进行取实部的操作
IK_real=tf.real(IK)
session=tf.Session()
print(session.run(IK_real))
[ 2.9999998 10. 3. -4. 10. 1.
-17. -6. ]
三.具备深度的一维离散卷积
1.具备深度的张量与卷积核的卷积
张量x可以理解为是一个长度为3,深度为3的张量,K可以理解为是一个长度为2,深度为3的张量,两者same卷积的过程就是锚点顺序移动到输入张量的每一个位置处,然后对应位置相乘,求和
注意:输入张量的深度和卷积核的深度是相等的
import tensorflow as tf
# 1个长度为3,深度为3的张量
x=tf.constant(
[
[[2,5,2],[6,1,-1],[7,9,-5]]
]
,tf.float32
)
# 1个长度为2,深度为3的卷积核
k=tf.constant(
[
[[-1],[5],[4]],[[2],[1],[6]]
]
,tf.float32
)
# 一维same卷积
v_conv1d_k=tf.nn.conv1d(x,k,1,'SAME')
session=tf.Session()
print(session.run(v_conv1d_k))
[[[ 38.]
[-12.]
[ 18.]]]
2.具备深度的张量分别与多个卷积核的卷积
同一个张量与多个卷积核的卷积本质上是该张量分别与每一个卷积核卷积,然后将每一个卷积结果在深度方向上连接在一起。以长度为3,深度为3的输入张量与2个长度为2,深度为3的卷积核卷积为例
import tensorflow as tf
x=tf.constant(
[
[[2,5,2],[6,1,-1],[7,9,-5]]
]
,tf.float32
)
# 2个长度为2,深度为3的卷积核
k=tf.constant(
[
[[-1,1],[5,3],[4,7]],[[2,-2],[1,-1],[6,9]]
]
,tf.float32
)
v_conv1d_k=tf.nn.conv1d(x,k,1,'SAME')
session=tf.Session()
print(session.run(v_conv1d_k))
[[[ 38. 9.]
[-12. -66.]
[ 18. -1.]]]
1个深度为C的张量与M个深度为C的卷积核的卷积结果的深度为M,即最后输出结果的深度与卷积核的个数相等
3.多个具备深度的张量分别与多个卷积核的卷积
计算3个长度为3,深度为3的张量与2个长度为2,深度为3的卷积核的卷积
import tensorflow as tf
# 3个长度为3,深度为3的张量
x=tf.constant(
[
[[2,5,2],[6,1,-1],[7,9,-5]], # 第1个
[[1,3,2],[5,2,-2],[8,4,3]], # 第2个
[[4,5,-1],[1,9,5],[2,7,0]] # 第3个
]
,tf.float32
)
# 2个长度为2,深度为3的卷积核
k=tf.constant(
[
[[-1,1],[5,3],[4,7]],[[2,-2],[1,-1],[6,9]]
]
,tf.float32
)
v_conv1d_k=tf.nn.conv1d(x,k,1,'SAME')
session=tf.Session()
print(session.run(v_conv1d_k))
[[[ 38. 9.]
[-12. -66.]
[ 18. -1.]]
[[ 22. -6.]
[ 35. 4.]
[ 24. 41.]]
[[ 58. 46.]
[ 75. 52.]
[ 33. 23.]]]
函数tf.nn.conv1d可以实现任意多个输入量分别与任意多个卷积核的卷积,输入张量的深度和卷积核的深度是相等的
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:Tensorflow–一维离散卷积 - Python技术站

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫