转自: https://www.cnblogs.com/hellcat/p/9687624.html
一、空洞卷积的提出
空洞卷积(atrous convolutions)又名扩张卷积(dilated convolutions),向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数,该参数定义了卷积核处理数据时各值的间距。
该结构的目的是在不用pooling(pooling层会导致信息损失)且计算量相当的情况下,提供更大的感受野。 顺便一提,卷积结构的主要问题如下:
池化层不可学
内部数据结构丢失;空间层级化信息丢失。
小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
而空洞卷积就有内部数据结构的保留和避免使用 down-sampling 这样的特性,优点明显。
二、空洞卷积原理
如下如,卷积核没有红点标记位置为0,红点标记位置同正常卷积核。
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/hjvQNOScuUtF20230407.jpg)
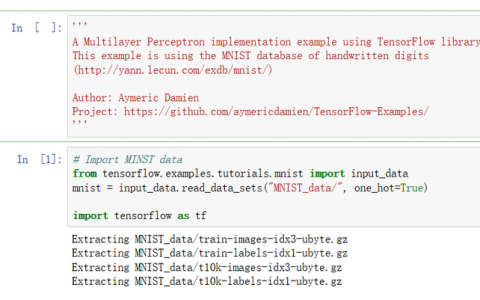
假设原始特征为feat0,首先使用扩张率为1的空洞卷积生成feat1,feat1上一点相对feat0感受野为3*3(如图a);
然后使用扩张率为2的空洞卷积处理feat1生成feat2(如图b),使第一次空洞卷积的卷积核大小等于第二次空洞卷积的一个像素点的感受野,图b即feat1上一个点综合了图a即feat0上3*3区域的信息,则生成的feat2感受野为7*7,即整个图b深色区域;
第三次处理同上,第二次空洞卷积的整个卷积核大小等于第三次空洞卷积的一个像素点的感受野,图c即feat2上每个点综合了feat0上7*7的信息(感受野),则采用扩张率为3的空洞卷积,生成的feat3每一个点感受野为15*15。
相比较之下,使用stride为1的普通3*3卷积,三层之后感受野仅仅为(kernel-1)*layer+1=7。
三、空洞卷积问题
感受野跳跃
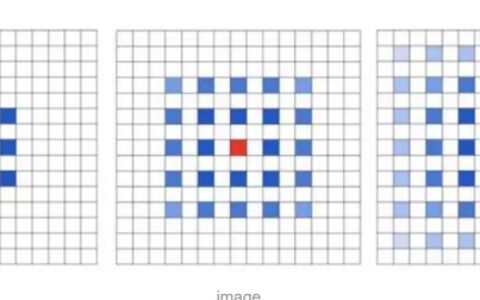
我们对同一张图连续三次使用扩张率为1的空洞卷积,观察整张图的中心点的感受野(如下图)
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/lkKKYKvcNnBe20230407.jpg)
很明显,感受野不连续(我们上一小结的例子就没这个问题,所以空洞卷积依赖网络设计)。
小尺度物体检测
类似第一个问题,仍然需要调整扩张率的组合来解决这个问题。
四、网络设计研究
第一个特性是,叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积,依然会出现 gridding effect。
第二个特性是,我们将 dilation rate 设计成 锯齿状结构,例如 [1, 2, 5, 1, 2, 5] 循环结构。
第三个特性是,我们需要满足一下这个式子: ![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/agIuKGGNlXEe20230407.jpg)
其中
是 i 层的 dilation rate 而
是指在 i 层的最大dilation rate,那么假设总共有n层的话,默认
。假设我们应用于 kernel 为 k x k 的话,我们的目标则是
,这样我们至少可以用 dilation rate 1 即 standard convolution 的方式来覆盖掉所有洞。
一个简单的例子: dilation rate [1, 2, 5] with 3 x 3 kernel (可行的方案):
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/RkWpJnPPgZKC20230407.jpg)
而这样的锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求(小 dilation rate 来关心近距离信息,大 dilation rate 来关心远距离信息)。
单分支设计的研究
通向标准化设计:Hybrid Dilated Convolution (HDC),可以很好的满足分割需要,如下图所示,
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/VBuFiZCxZExp20230407.jpg)
多分支研究解决多尺度分割
仅仅(在一个卷积分支网络下)使用 dilated convolution 去抓取多尺度物体是一个不正统的方法。比方说,我们用一个 HDC 的方法来获取一个大(近)车辆的信息,然而对于一个小(远)车辆的信息都不再受用。假设我们再去用小 dilated convolution 的方法重新获取小车辆的信息,则这么做非常的冗余。
基于港中文和商汤组的 PSPNet 里的 Pooling module (其网络同样获得当年的SOTA结果),ASPP 则在网络 decoder 上对于不同尺度上用不同大小的 dilation rate 来抓去多尺度信息,每个尺度则为一个独立的分支,在网络最后把他合并起来再接一个卷积层输出预测 label。这样的设计则有效避免了在 encoder 上冗余的信息的获取,直接关注与物体之间之内的相关性。
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/HOaHVfOkWQtl20230407.jpg)
五、常用框架API介绍
TensorFlow接口
tf.nn.atrous_conv2d(value, filters, rate, padding, name=None)
value: 指需要做卷积的输入图像,要求是一个4维Tensor,具有[batch, height, width, channels]这样的shape,具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]
filters: 相当于CNN中的卷积核,要求是一个4维Tensor,具有[filter_height, filter_width, channels, out_channels]这样的shape,具体含义是[卷积核的高度,卷积核的宽度,图像通道数,卷积核个数],同理这里第三维channels,就是参数value的第四维
rate: 要求是一个int型的正数,正常的卷积操作应该会有stride(即卷积核的滑动步长),但是空洞卷积是没有stride参数的,这一点尤其要注意。取而代之,它使用了新的rate参数,那么rate参数有什么用呢?它定义为我们在输入图像上卷积时的采样间隔,你可以理解为卷积核当中穿插了(rate-1)数量的“0”,把原来的卷积核插出了很多“洞洞”,这样做卷积时就相当于对原图像的采样间隔变大了。具体怎么插得,可以看后面更加详细的描述。此时我们很容易得出rate=1时,就没有0插入,此时这个函数就变成了普通卷积。
padding: string类型的量,只能是”SAME”,”VALID”其中之一,这个值决定了不同边缘填充方式。
函数默认stride=1,无法改变。
结果返回一个Tensor,填充方式为“VALID”时,返回[batch,height-2*(filter_width-1),width-2*(filter_height-1),out_channels]的Tensor,填充方式为“SAME”时,返回[batch, height, width, out_channels]的Tensor。
测试代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
img = tf.constant(value=[[[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]]]],dtype=tf.float32)
img = tf.concat(values=[img,img],axis=3)
filter = tf.constant(value=1, shape=[3,3,2,5], dtype=tf.float32)
out_img1 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1, padding='SAME')
out_img2 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1, padding='VALID')
out_img3 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='SAME')
#error #out_img4 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='VALID') with tf.Session() as sess: print('rate=1, SAME mode result:')
print(sess.run(out_img1))
print('rate=1, VALID mode result:')
print(sess.run(out_img2))
print('rate=2, SAME mode result:')
print(sess.run(out_img3)) # error #print 'rate=2, VALID mode result:' #print(sess.run(out_img4))
|
扩张率为1时,空洞卷积等价于普通卷积。对于SAME和VALID模式计算方式如下图所示,
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/PtfbJrtsyoRy20230407.jpg)
扩张率为2的VALID模式计算过程,
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/KKlGLgDZEwPV20230407.jpg)
扩张率为2的VALID模式会报错,此时卷积核大于图片,无法卷积。
MXNet接口
MXNet卷积操作自带扩张率参数,详见文档。
MXNet的通道存储与TensorFlow不太一致,所以我们打印一下(对比上面的图,可以体会到为什么除了tf外大多框架把通道放在第二维),
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import mxnet as mx
import mxnet.ndarray as nd
img = nd.array([[[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]]]])
img = nd.concat(img, img, dim=-1)
img = nd.transpose(img, axes=(0, 3, 1, 2))
w = nd.ones([5, 2, 3, 3])
b = nd.array([0 for _ in range(5)])
img |
[[[[1. 2. 3. 4.] [1. 2. 3. 4.] [1. 2. 3. 4.] [1. 2. 3. 4.]][[1. 2. 3. 4.]
[1. 2. 3. 4.]
[1. 2. 3. 4.]
[1. 2. 3. 4.]]]]
<NDArray 1x2x4x4 @cpu(0)>
|
1
|
nd.Convolution(img, w, b, kernel=w.shape[2:], num_filter=w.shape[0], stride=(1, 1), pad=(1,1), dilate=(1,1))
|
[[[[12. 24. 36. 28.] [18. 36. 54. 42.] [18. 36. 54. 42.] [12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]]]]
<NDArray 1x5x4x4 @cpu(0)>
|
1
|
nd.Convolution(img, w, b, kernel=w.shape[2:], num_filter=w.shape[0], stride=(1, 1), pad=(2,2), dilate=(2,2))
|
[[[[16. 24. 16. 24.] [16. 24. 16. 24.] [16. 24. 16. 24.] [16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]]]]
<NDArray 1x5x4x4 @cpu(0)>
六、参考来源
Multi-scale Context Aggregation by Dilated Convolutions
【Tensorflow】tf.nn.atrous_conv2d如何实现空洞卷积?
如何理解空洞卷积(dilated convolution)?
一、空洞卷积的提出
空洞卷积(atrous convolutions)又名扩张卷积(dilated convolutions),向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数,该参数定义了卷积核处理数据时各值的间距。
该结构的目的是在不用pooling(pooling层会导致信息损失)且计算量相当的情况下,提供更大的感受野。 顺便一提,卷积结构的主要问题如下:
池化层不可学
内部数据结构丢失;空间层级化信息丢失。
小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
而空洞卷积就有内部数据结构的保留和避免使用 down-sampling 这样的特性,优点明显。
二、空洞卷积原理
如下如,卷积核没有红点标记位置为0,红点标记位置同正常卷积核。
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/wvehecDYIMjO20230407.jpg)
假设原始特征为feat0,首先使用扩张率为1的空洞卷积生成feat1,feat1上一点相对feat0感受野为3*3(如图a);
然后使用扩张率为2的空洞卷积处理feat1生成feat2(如图b),使第一次空洞卷积的卷积核大小等于第二次空洞卷积的一个像素点的感受野,图b即feat1上一个点综合了图a即feat0上3*3区域的信息,则生成的feat2感受野为7*7,即整个图b深色区域;
第三次处理同上,第二次空洞卷积的整个卷积核大小等于第三次空洞卷积的一个像素点的感受野,图c即feat2上每个点综合了feat0上7*7的信息(感受野),则采用扩张率为3的空洞卷积,生成的feat3每一个点感受野为15*15。
相比较之下,使用stride为1的普通3*3卷积,三层之后感受野仅仅为(kernel-1)*layer+1=7。
三、空洞卷积问题
感受野跳跃
我们对同一张图连续三次使用扩张率为1的空洞卷积,观察整张图的中心点的感受野(如下图)
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/bvLmuucxrgih20230407.jpg)
很明显,感受野不连续(我们上一小结的例子就没这个问题,所以空洞卷积依赖网络设计)。
小尺度物体检测
类似第一个问题,仍然需要调整扩张率的组合来解决这个问题。
四、网络设计研究
第一个特性是,叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积,依然会出现 gridding effect。
第二个特性是,我们将 dilation rate 设计成 锯齿状结构,例如 [1, 2, 5, 1, 2, 5] 循环结构。
第三个特性是,我们需要满足一下这个式子: ![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/nKhFDvVnPCkY20230407.jpg)
其中
是 i 层的 dilation rate 而
是指在 i 层的最大dilation rate,那么假设总共有n层的话,默认
。假设我们应用于 kernel 为 k x k 的话,我们的目标则是
,这样我们至少可以用 dilation rate 1 即 standard convolution 的方式来覆盖掉所有洞。
一个简单的例子: dilation rate [1, 2, 5] with 3 x 3 kernel (可行的方案):
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/PxaRDpGhszEi20230407.jpg)
而这样的锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求(小 dilation rate 来关心近距离信息,大 dilation rate 来关心远距离信息)。
单分支设计的研究
通向标准化设计:Hybrid Dilated Convolution (HDC),可以很好的满足分割需要,如下图所示,
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/tbuMJZoxUNuS20230407.jpg)
多分支研究解决多尺度分割
仅仅(在一个卷积分支网络下)使用 dilated convolution 去抓取多尺度物体是一个不正统的方法。比方说,我们用一个 HDC 的方法来获取一个大(近)车辆的信息,然而对于一个小(远)车辆的信息都不再受用。假设我们再去用小 dilated convolution 的方法重新获取小车辆的信息,则这么做非常的冗余。
基于港中文和商汤组的 PSPNet 里的 Pooling module (其网络同样获得当年的SOTA结果),ASPP 则在网络 decoder 上对于不同尺度上用不同大小的 dilation rate 来抓去多尺度信息,每个尺度则为一个独立的分支,在网络最后把他合并起来再接一个卷积层输出预测 label。这样的设计则有效避免了在 encoder 上冗余的信息的获取,直接关注与物体之间之内的相关性。
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/AbwAqsZcfsTc20230407.jpg)
五、常用框架API介绍
TensorFlow接口
tf.nn.atrous_conv2d(value, filters, rate, padding, name=None)
value: 指需要做卷积的输入图像,要求是一个4维Tensor,具有[batch, height, width, channels]这样的shape,具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]
filters: 相当于CNN中的卷积核,要求是一个4维Tensor,具有[filter_height, filter_width, channels, out_channels]这样的shape,具体含义是[卷积核的高度,卷积核的宽度,图像通道数,卷积核个数],同理这里第三维channels,就是参数value的第四维
rate: 要求是一个int型的正数,正常的卷积操作应该会有stride(即卷积核的滑动步长),但是空洞卷积是没有stride参数的,这一点尤其要注意。取而代之,它使用了新的rate参数,那么rate参数有什么用呢?它定义为我们在输入图像上卷积时的采样间隔,你可以理解为卷积核当中穿插了(rate-1)数量的“0”,把原来的卷积核插出了很多“洞洞”,这样做卷积时就相当于对原图像的采样间隔变大了。具体怎么插得,可以看后面更加详细的描述。此时我们很容易得出rate=1时,就没有0插入,此时这个函数就变成了普通卷积。
padding: string类型的量,只能是”SAME”,”VALID”其中之一,这个值决定了不同边缘填充方式。
函数默认stride=1,无法改变。
结果返回一个Tensor,填充方式为“VALID”时,返回[batch,height-2*(filter_width-1),width-2*(filter_height-1),out_channels]的Tensor,填充方式为“SAME”时,返回[batch, height, width, out_channels]的Tensor。
测试代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
img = tf.constant(value=[[[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]]]],dtype=tf.float32)
img = tf.concat(values=[img,img],axis=3)
filter = tf.constant(value=1, shape=[3,3,2,5], dtype=tf.float32)
out_img1 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1, padding='SAME')
out_img2 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1, padding='VALID')
out_img3 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='SAME')
#error #out_img4 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='VALID') with tf.Session() as sess: print('rate=1, SAME mode result:')
print(sess.run(out_img1))
print('rate=1, VALID mode result:')
print(sess.run(out_img2))
print('rate=2, SAME mode result:')
print(sess.run(out_img3)) # error #print 'rate=2, VALID mode result:' #print(sess.run(out_img4))
|
扩张率为1时,空洞卷积等价于普通卷积。对于SAME和VALID模式计算方式如下图所示,
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/hfECVhRwzAgS20230407.jpg)
扩张率为2的VALID模式计算过程,
![[卷积核]空洞卷积(转) [卷积核]空洞卷积(转)](https://pythonjishu.com/wp-content/uploads/2023/04/LqwwMYZqKXag20230407.jpg)
扩张率为2的VALID模式会报错,此时卷积核大于图片,无法卷积。
MXNet接口
MXNet卷积操作自带扩张率参数,详见文档。
MXNet的通道存储与TensorFlow不太一致,所以我们打印一下(对比上面的图,可以体会到为什么除了tf外大多框架把通道放在第二维),
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import mxnet as mx
import mxnet.ndarray as nd
img = nd.array([[[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]],
[[1],[2],[3],[4]]]])
img = nd.concat(img, img, dim=-1)
img = nd.transpose(img, axes=(0, 3, 1, 2))
w = nd.ones([5, 2, 3, 3])
b = nd.array([0 for _ in range(5)])
img |
[[[[1. 2. 3. 4.] [1. 2. 3. 4.] [1. 2. 3. 4.] [1. 2. 3. 4.]][[1. 2. 3. 4.]
[1. 2. 3. 4.]
[1. 2. 3. 4.]
[1. 2. 3. 4.]]]]
<NDArray 1x2x4x4 @cpu(0)>
|
1
|
nd.Convolution(img, w, b, kernel=w.shape[2:], num_filter=w.shape[0], stride=(1, 1), pad=(1,1), dilate=(1,1))
|
[[[[12. 24. 36. 28.] [18. 36. 54. 42.] [18. 36. 54. 42.] [12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]][[12. 24. 36. 28.]
[18. 36. 54. 42.]
[18. 36. 54. 42.]
[12. 24. 36. 28.]]]]
<NDArray 1x5x4x4 @cpu(0)>
|
1
|
nd.Convolution(img, w, b, kernel=w.shape[2:], num_filter=w.shape[0], stride=(1, 1), pad=(2,2), dilate=(2,2))
|
[[[[16. 24. 16. 24.] [16. 24. 16. 24.] [16. 24. 16. 24.] [16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]][[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]
[16. 24. 16. 24.]]]]
<NDArray 1x5x4x4 @cpu(0)>
六、参考来源
Multi-scale Context Aggregation by Dilated Convolutions
【Tensorflow】tf.nn.atrous_conv2d如何实现空洞卷积?
如何理解空洞卷积(dilated convolution)?
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:[卷积核]空洞卷积(转) - Python技术站

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫