BZOJ 4827 循环卷积

题意：求两个手环任意旋转对应位置的差值+c的平方最小

设b旋转到k最小，那么先将b扩张一倍构成一圈，那么答案式子就是

                               

 

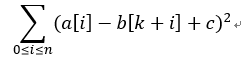
将这个式子展开一下，事情就变得有趣了起来

 

 

 

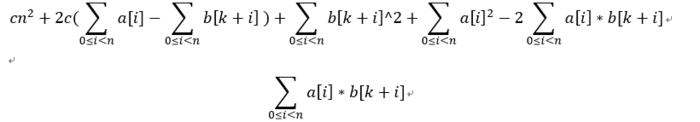
                                  　　　　　　这个式子将a[ ]翻转可以化成卷积形式

                                   

 

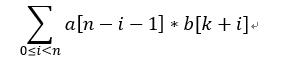
直接套上一个FFT就可以了

然后枚举C就行了（C的范围比较小，主要是写起来容易，追求效率可以用求根公式算出这个二次函数取得最小值的时候，C的大小）

 

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <queue>
  4 #include <cmath>
  5 #include <algorithm>
  6 #include <set>
  7 #include <iostream>
  8 #include <map>
  9 #include <stack>
 10 #include <string>
 11 #include <vector>
 12 #define  pi acos(-1.0)
 13 #define  eps 1e-9
 14 #define  fi first
 15 #define  se second
 16 #define  rtl   rt<<1
 17 #define  rtr   rt<<1|1
 18 #define  bug         printf("******n")
 19 #define  mem(a,b)    memset(a,b,sizeof(a))
 20 #define  name2str(x) #x
 21 #define  fuck(x)     cout<<#x" = "<<x<<endl
 22 #define  f(a)        a*a
 23 #define  sf(n)       scanf("%d", &n)
 24 #define  sff(a,b)    scanf("%d %d", &a, &b)
 25 #define  sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
 26 #define  sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d)
 27 #define  pf          printf
 28 #define  FRE(i,a,b)  for(i = a; i <= b; i++)
 29 #define  FREE(i,a,b) for(i = a; i >= b; i--)
 30 #define  FRL(i,a,b)  for(i = a; i < b; i++)+
 31 #define  FRLL(i,a,b) for(i = a; i > b; i--)
 32 #define  FIN         freopen("data.txt","r",stdin)
 33 #define  gcd(a,b)    __gcd(a,b)
 34 #define  lowbit(x)   x&-x
 35 #define rep(i,a,b) for(int i=a;i<b;++i)
 36 #define per(i,a,b) for(int i=a-1;i>=b;--i)
 37 using namespace std;
 38 typedef long long  LL;
 39 typedef unsigned long long ULL;
 40 const int maxn = 3e5 + 7;
 41 const int maxm = maxn * 4;
 42 const int mod = 1e9 + 7;
 43 int n, m, a[maxn], b[maxn];
 44 int len, res[maxm], mx; //开大4倍
 45 struct cpx {
 46     long double r, i;
 47     cpx ( long double r = 0, long double i = 0 ) : r ( r ), i ( i ) {};
 48     cpx operator+ ( const cpx &b ) {
 49         return cpx ( r + b.r, i + b.i );
 50     }
 51     cpx operator- ( const cpx &b ) {
 52         return cpx ( r - b.r, i - b.i );
 53     }
 54     cpx operator* ( const cpx &b ) {
 55         return cpx ( r * b.r - i * b.i, i * b.r + r * b.i );
 56     }
 57 } va[maxm], vb[maxm];
 58 void rader ( cpx F[], int len ) { //len = 2^M,reverse F[i] with  F[j] j为i二进制反转
 59     int j = len >> 1;
 60     for ( int i = 1; i < len - 1; ++i ) {
 61         if ( i < j ) swap ( F[i], F[j] ); // reverse
 62         int k = len >> 1;
 63         while ( j >= k ) j -= k, k >>= 1;
 64         if ( j < k ) j += k;
 65     }
 66 }
 67 void FFT ( cpx F[], int len, int t ) {
 68     rader ( F, len );
 69     for ( int h = 2; h <= len; h <<= 1 ) {
 70         cpx wn ( cos ( -t * 2 * pi / h ), sin ( -t * 2 * pi / h ) );
 71         for ( int j = 0; j < len; j += h ) {
 72             cpx E ( 1, 0 ); //旋转因子
 73             for ( int k = j; k < j + h / 2; ++k ) {
 74                 cpx u = F[k];
 75                 cpx v = E * F[k + h / 2];
 76                 F[k] = u + v;
 77                 F[k + h / 2] = u - v;
 78                 E = E * wn;
 79             }
 80         }
 81     }
 82     if ( t == -1 ) //IDFT
 83         for ( int i = 0; i < len; ++i ) F[i].r /= len;
 84 }
 85 void Conv ( cpx a[], cpx b[], int len ) { //求卷积
 86     FFT ( a, len, 1 );
 87     FFT ( b, len, 1 );
 88     for ( int i = 0; i < len; ++i ) a[i] = a[i] * b[i];
 89     FFT ( a, len, -1 );
 90 }
 91 void gao () {
 92     len = 1;
 93     mx = n + m;
 94     while ( len <= mx ) len <<= 1; //mx为卷积后最大下标
 95     for ( int i = 0; i < len; i++ ) va[i].r = va[i].i = vb[i].r = vb[i].i = 0;
 96     for ( int i = 0; i < n; i++ ) va[i].r = a[i]; //根据题目要求改写
 97     for ( int i = 0; i < m; i++ ) vb[i].r = b[i]; //根据题目要求改写
 98     Conv ( va, vb, len );
 99     for ( int i = 0; i < len; ++i ) res[i] += ( LL ) floor ( va[i].r + 0.5 );
100 }
101 
102 int main() {
103    // FIN;
104     sff ( n, m );
105     int suma = 0, sumb = 0, sum1 = 0, sum2 = 0;
106     for ( int i = 0 ; i < n ; i++ ) sf ( a[n - 1 - i] ), suma += a[n - 1 - i], sum1 += a[n - 1 - i] * a[n - 1 - i];
107     for ( int i = 0 ; i < n ; i++ ) sf ( b[i] ), b[n + i] = b[i], sumb += b[i], sum2 += b[i] * b[i];
108     m = 2 * n;
109     gao();
110     LL cnt = 0, ans = 0x3f3f3f3f3f3fLL;
111     for ( int i = n ; i < 2 * n ; i++ ) cnt = max ( cnt, 1LL * res[i] );
112     //fuck ( cnt );
113     for ( int i = -m ; i <= m ; i++ )
114         ans = min ( ans, 1LL * i * i * n + 1LL * 2 * i * ( suma - sumb ) + sum1 + sum2 - 1LL * 2 * cnt );
115     printf ( "%lldn", ans );
116     return 0;
117 }