一、BPR算法的原理：

1、贝叶斯个性化排序(BPR)算法小结
https://www.cnblogs.com/pinard/p/9128682.html
2、Bayesian Personalized Ranking 算法解析及Python实现
https://www.cnblogs.com/wkang/p/10217172.html
3、推荐系统中的排序学习
https://lumingdong.cn/learning-to-rank-in-recommendation-system.html?unapproved=401&moderation-hash=fcc3652917e1688fe59997e11c916297#配对法（Pairwise）
4、Recommender system using Bayesian personalized ranking
https://towardsdatascience.com/recommender-system-using-bayesian-personalized-ranking-d30e98bba0b9
5、推荐算法之贝叶斯个性化排序 BPR
https://www.biaodianfu.com/bpr.html

二、算法中的注意点

根据完整性和反对称性，优化目标的第一部分

[prod_{u in U}P(>_u|theta) = prod_{(u,i,j) in (U times I times I)}P(i >_u j|theta)^{delta((u,i,j) in Ds)}(1-P(i >_u j|theta))^{delta((u,j,i) notin Ds) }
]

[delta(b)= begin{cases} 1& {if; b; is ;true}\ 0& {else} end{cases}
]

可以简化为：

[prod_{u in U}P(>_u|theta) = prod_{(u,i,j) in Ds}P(i >_u j|theta)
]

如何理解这个转换：
1、((u,i,j) in (U times I times I))情况下，(P(i >_u j|theta)^{delta((u,i,j) in Ds)})和((1-P(i >_u j|theta))^{delta((u,j,i) notin Ds) })提供了相同的信息。

这句话又如何理解：
论文中的训练集(Ds：=left{(u,i,j)| i in I_u^+ cap j in I backslash I_u^+ right}),由于加了限定条件因为$（u，i，j） $中的 (i) 和 (j) 都是有限制的。。
其中 ((u,i,j) in Ds) 的表示是用户 (u) 更喜欢 (i) 胜过(j)；(cap) 是表示交集；(I backslash I_u^+) 表示物品集(I)除正例外其他剩余的样本，即用户没有评分过的item。
((u, i, j))只能取特定的值，而不是遍历整个三维数组(1, 1, 1)-(m, n, n)。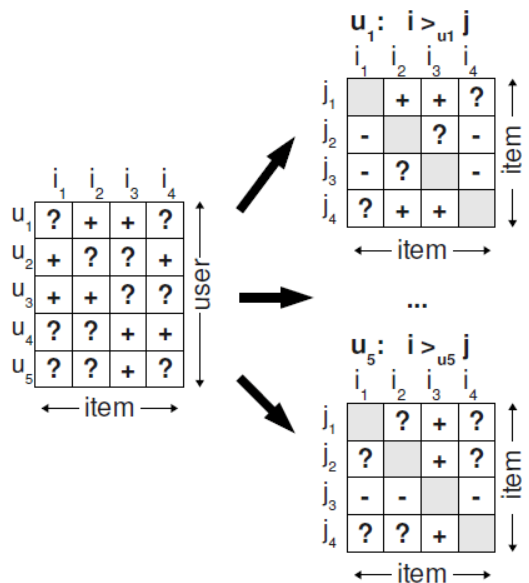
贝叶斯个性化排序(BPR)pytorch实现
以(u_1)为例，其训练集合(Ds={(u1,i2,j1),(u1,i2,j4),(u1,i3,j1),(u1,i3,j4)})
根据 (u1×I×I)，它的负例为:({(u,j,i)∉ Ds}:={(u1,j2,i1),(u1,j2,i4),(u1,j3,i1),(u1,j3,i4)})。
可见(i，j)互换了位置。因此当第二部分的指数部分为1时:((u,j,i) notin D_s)，必有((u,i,j) in Ds)。即当负例存在的时候，正例必定存在。所以，二者提供了相同的信息。
2、只有当((u,i,j) in Ds)时，({delta((u,i,j) in Ds =1})，因此可以完成上述转换。

三、pytorch实现

源码来自： https://github.com/guoyang9/BPR-pytorch
1、读取数据

import numpy as np 
import pandas as pd 
import scipy.sparse as sp
import torch.utils.data as data
import torch
import torch.nn as nn
import os
import time
dataset = 'ml-1m'
main_path = './Data/'
train_rating = main_path + '{}.train.rating'.format(dataset)
test_rating = main_path + '{}.test.rating'.format(dataset)
test_negative = main_path + '{}.test.negative'.format(dataset)
model_path = './models/'
BPR_model_path = model_path + 'BPR.pth'

# 1、训练集
train_data = pd.read_csv(train_rating, sep='t', header=None, names=['user', 'item'], 
    usecols=[0, 1], dtype={0: np.int32, 1: np.int32})

user_num = train_data['user'].max() + 1
item_num = train_data['item'].max() + 1
train_data = train_data.values.tolist()
# 2、训练样本转换为稀疏矩阵
train_mat = sp.dok_matrix((user_num, item_num), dtype=np.float32)
for x in train_data:
    train_mat[x[0], x[1]] = 1.0

# 3、测试集数据读取,即为每个用户赋值99个没评分过的item。 1个评分过的+99个未评分的。
test_data = []
with open(test_negative, 'r') as fd:
    line = fd.readline()
    while line != None and line != '':
        arr = line.split('t')
        u = eval(arr[0])[0]
        test_data.append([u, eval(arr[0])[1]])
        for i in arr[1:]:
            test_data.append([u, int(i)])
        line = fd.readline()

2、构建BPR数据类

# 根据继承pytorch的Dataset类定义BPR数据类
class BPRData(data.Dataset):
    def __init__(self, features,
                 num_item, train_mat=None, num_ng=0, is_training=None):
        """features=train_data,num_item=item_num,train_mat，稀疏矩阵，num_ng,训练阶段默认为4，即采样4-1个负样本对应一个评分过的
        数据。
        """
        super(BPRData, self).__init__()
        """ Note that the labels are only useful when training, we thus 
            add them in the ng_sample() function.
        """
        self.features = features
        self.num_item = num_item
        self.train_mat = train_mat
        self.num_ng = num_ng
        self.is_training = is_training

    def ng_sample(self):
        assert self.is_training, 'no need to sampling when testing'

        self.features_fill = []
        for x in self.features:
            u, i = x[0], x[1]
            for t in range(self.num_ng):
                j = np.random.randint(self.num_item)
                while (u, j) in self.train_mat:
                    j = np.random.randint(self.num_item)
                self.features_fill.append([u, i, j])

    def __len__(self):
        return self.num_ng * len(self.features) if 
            self.is_training else len(self.features)

    def __getitem__(self, idx):
        features = self.features_fill if 
            self.is_training else self.features

        user = features[idx][0]
        item_i = features[idx][1]
        item_j = features[idx][2] if 
            self.is_training else features[idx][1]
        return user, item_i, item_j

3、生成DataLoader

train_dataset = BPRData(
        train_data, item_num, train_mat, 4, True)
test_dataset = BPRData(
        test_data, item_num, train_mat, 0, False)
train_loader = data.DataLoader(train_dataset,
                                   batch_size=4096, shuffle=True, num_workers=0)
test_loader = data.DataLoader(test_dataset,
                                  batch_size=100, shuffle=False, num_workers=0)

4、定义BPR模型，完成前向传播过程

class BPR(nn.Module):
    def __init__(self, user_num, item_num, factor_num):
        super(BPR, self).__init__()
        """
        user_num: number of users;
        item_num: number of items;
        factor_num: number of predictive factors.
        """
        self.embed_user = nn.Embedding(user_num, factor_num)
        self.embed_item = nn.Embedding(item_num, factor_num)

        nn.init.normal_(self.embed_user.weight, std=0.01)
        nn.init.normal_(self.embed_item.weight, std=0.01)

    def forward(self, user, item_i, item_j):
        user = self.embed_user(user)
        item_i = self.embed_item(item_i)
        item_j = self.embed_item(item_j)

        prediction_i = (user * item_i).sum(dim=-1)
        prediction_j = (user * item_j).sum(dim=-1)
        return prediction_i, prediction_j
model = BPR(user_num, item_num, 16)
model.cuda()

5、定义优化器

import torch.optim as optim
lamb = 0.001
lr = 0.01
optimizer = optim.SGD(model.parameters(), lr=lr, weight_decay=lamb)

6、定义一些评价指标

def hit(gt_item, pred_items):
    if gt_item in pred_items:
        return 1
    return 0


def ndcg(gt_item, pred_items):
    if gt_item in pred_items:
        index = pred_items.index(gt_item)
        return np.reciprocal(np.log2(index+2))
    return 0


def metrics(model, test_loader, top_k):
    HR, NDCG = [], []

    for user, item_i, item_j in test_loader:
        user = user.cuda()
        item_i = item_i.cuda()
        item_j = item_j.cuda() # not useful when testing

        prediction_i, prediction_j = model(user, item_i, item_j)
        _, indices = torch.topk(prediction_i, top_k)
        recommends = torch.take(
            item_i, indices).cpu().numpy().tolist()

        gt_item = item_i[0].item()
        HR.append(hit(gt_item, recommends))
        NDCG.append(ndcg(gt_item, recommends))
    return np.mean(HR), np.mean(NDCG)

7、训练和测试

# 6、训练过程，根据公式得到后验概率，然后求导，更新两个矩阵的值。
import os
epochs = 50
top_k = 10
best_hr = 0 # 记录命中率。
import time
for epoch in range(epochs):
    model.train() # 在使用pytorch构建神经网络的时候，训练过程中会在程序上方添加一句model.train()，作用是启用batch normalization和drop out。
    start_time = time.time()
    train_loader.dataset.ng_sample() # 训练阶段，这一步生成真正的训练样本
    for user,item_i,item_j in train_loader:
        user = user.cuda()
        item_i = item_i.cuda()
        item_j = item_j.cuda()
        model.zero_grad()
        prediction_i,prediction_j = model(user,item_i,item_j) # 调用forward()方法
        loss = -(prediction_i-prediction_j).sigmoid().log().sum() # 这里是最小化取了负号后对应的对数后验估计函数。可以使用梯度下降。
        loss.backward() # 在这里得到梯度
        optimizer.step() # 根据上面得到的梯度进行梯度回传。
    # 一个epoch训练结束，开始测试
    model.eval() # 测试过程中会使用model.eval()，这时神经网络会沿用batch normalization的值，并不使用drop out。
    HR, NDCG = metrics(model, test_loader, top_k)
    elapsed_time = time.time() - start_time
    print("The time elapse of epoch {:03d}".format(epoch) + " is: " +
         time.strftime("%H: %M: %S", time.gmtime(elapsed_time)))
    print("HR: {:.3f}tNDCG: {:.3f}".format(np.mean(HR), np.mean(NDCG)))
    if HR > best_hr:
        best_hr,best_ndcg,best_epoch = HR,NDCG,epoch
        if not os.path.exists(model_path):
            os.mkdir(model_path)
        torch.save(model,'{}BPR.pt'.format(model_path))
print("End. Best epoch {:03d}: HR = {:.3f}, NDCG = {:.3f}".format(best_epoch, best_hr, best_ndcg))