手把手教你理解和实现生成式对抗神经网络（GAN）

一、总结

一句话总结：

GAN的全称是 Generative Adversarial Networks，中文名称是生成对抗网络。原始的GAN是一种无监督学习方法，巧妙的利用“博弈”的思想来学习生成式模型。

 

 

1、gan的目标函数？

$$min _ { G } max _ { D } V ( D , G ) = E _ { x sim p _ { text { data } } ( x ) } [ log D ( x ) ] + E _ { z sim p _ { z } ( z ) } [ log ( 1 - D ( G ( z ) ) ) ]$$

 

 

2、gan对抗神经网络的讲解思路？

（由简来讲一些看起来比较复杂的问题）gan对抗神经网络的讲解思路可以没必要直接从生成图片着手，可以从生成普通函数开始，比如一个普通的二次函数

 

 

 

二、手把手教你理解和实现生成式对抗神经网络（GAN）

转自或参考：手把手教你理解和实现生成式对抗神经网络（GAN）
https://zhuanlan.zhihu.com/p/43047326

 

生成式对抗神经网络（GAN）是目前深度学习研究中最活跃的领域之一，原因正是其能够生成非常逼真的合成结果。在本文，我们会学习 GAN 的工作原理，然后用 TensorFlow 实现一个简单的 GAN。文章结构如下：

• GAN 的基本理念和工作原理
• 实现一个 GAN 模型，能从一个简单分布中生成数据
• 可视化和分析 GAN 的各个方面，更好地理解其背后原理

 

本文代码地址见文末。

 

GAN 工作原理

GAN 的基本理念其实非常简单，其核心由两个目标互相冲突的神经网络组成，这两个网络会以越来越复杂的方法来“蒙骗”对方。这种情况可以理解为博弈论中的极大极小博弈树。

 

我们以一个伪造货币的例子形象地解释 GAN 的工作原理。

在这个过程中，我们想象有两类人：警察和罪犯。我们看看他们的之间互相冲突的目标：

• 罪犯的目标：他的主要目标就是想出伪造货币的复杂方法，从而让警察无法区分假币和真币。
• 警察的目标：他的主要目标就是想出辨别货币的复杂方法，这样就能够区分假币和真币。

 

随着这个过程不断继续，警察会想出越来越复杂的技术来鉴别假币，罪犯也会想出越来越复杂的技术来伪造货币。这就是 GAN 中“对抗过程”的基本理念。

 

GAN 充分利用“对抗过程”训练两个神经网络，这两个网络会互相博弈直至达到一种理想的平衡状态，我们这个例子中的警察和罪犯就相当于这两个神经网络。其中一个神经网络叫做生成器网络 G（Z），它会使用输入随机噪声数据，生成和已有数据集非常接近的数据；另一个神经网络叫鉴别器网络 D（X），它会以生成的数据作为输入，尝试鉴别出哪些是生成的数据，哪些是真实数据。鉴别器的核心是实现二元分类，输出的结果是输入数据来自真实数据集（和合成数据或虚假数据相对）的概率。

 

整个过程的目标函数从正式意义上可以写为：

 

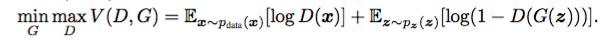
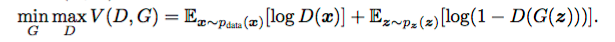
我们在前面所说的 GAN 最终能达到一种理想的平衡状态，是指生成器应该能模拟真实的数据，鉴别器输出的概率应该为 0.5， 即生成的数据和真实数据一致。也就是说，它不确定来自生成器的新数据是真实还是虚假，二者的概率相等。

 

你可能很好奇，为什么我们会需要这么复杂的学习过程？学习这样一种模型的好处是什么？

GAN 的创造者 Ian Goodfellow 曾提到过，GAN 以及所有生成方法的背后灵感源自著名物理学家理查德·费曼的一句名言：

 

 

我不能创造的东西，我就不理解（What I cannot create, I do not understand）。

 

当然 Ian Googfellow 这里指的是机器：“AI不能创造的东西，它就不理解。”

 

这是息息相关的，因为如果我们能从模型中生成真实的数据分布，那么就意味着我们能知道理解该模型的方方面面的信息。大多时候，这些真实的数据分布包含数百万张图像，我们可以用具有数千个参数的模型生成它们，模型的这些参数能够捕捉给定图像的本质。

 

在实际生活中，GAN 有很多用途，我们在后面会讲到。

 

实现 GAN

在这部分，我们会生成一个非常简单的数据分布，试着学习一个生成器函数，它会用 GAN 模型从该数据分布中生成数据。整个部分分成 3 个小部分。首先，我们会写一个基本函数生成一个二次型分布（真实数据分布），然后，我们写一个生成器以及一个鉴别器。最后我们会用数据以对抗的方式训练这两个神经网络。

 

本次实现的目标就是学习一种新函数，能够从和训练数据一样的分布中生成数据。我们预期训练中生成器网络应当能生成遵循二次型分布的数据，这里在下个部分会更详细的解释。虽然我们是以非常简单的数据分布着手，但 GAN 很容易地能延伸为从很复杂的数据集中生成数据，比如生成手写字、明星脸部、动物等等。

 

生成训练数据

我们通过用 Numpy 库生成随机样本，然后用一种函数生成第二个数据分布来实现我们的真实数据集。为了简单起见，我们将函数设为二次函数。当然你可以用这里的代码生成具有更多维度或特征之间关系更为复杂的数据集。

import numpy as np

def get_y(x):
    return 10 + x*x

def sample_data(n=10000, scale=100):
    data = []

    x = scale*(np.random.random_sample((n,))-0.5)

    for i in range(n):
        yi = get_y(x[i])
        data.append([x[i], yi])

    return np.array(data)

 

生成的数据非常简单，画出来会如下所示：

 

 

 

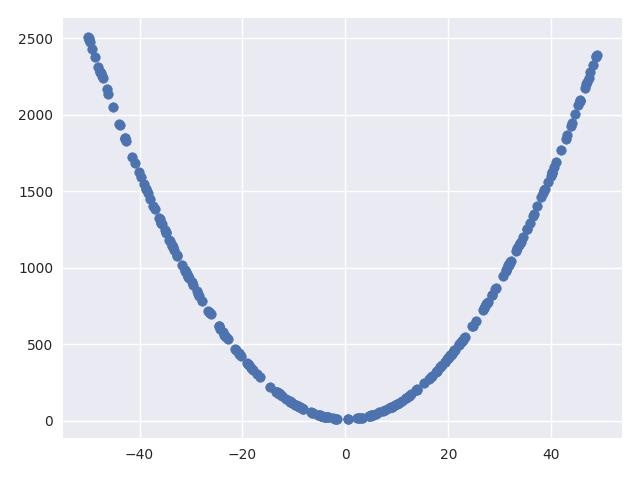
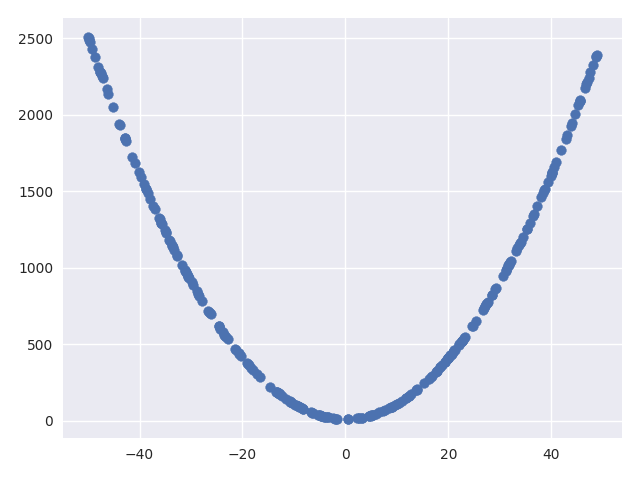
实现生成器和鉴别器网络

 

我们现在用 TensorFlow 层实现生成器和鉴别器网络。首先用如下函数实现生成器网络：

 

def generator(Z,hsize=[16, 16],reuse=False):
    with tf.variable_scope("GAN/Generator",reuse=reuse):
        h1 = tf.layers.dense(Z,hsize[0],activation=tf.nn.leaky_relu)
        h2 = tf.layers.dense(h1,hsize[1],activation=tf.nn.leaky_relu)
        out = tf.layers.dense(h2,2)

return out

 

该函数以 placeholder 为随机样本（Z），数组 hsize 为 2 个隐藏层中的神经元数量，变量 reuse 则用于重新使用同样的网络层。使用这些输入，函数会创建一个具有 2 个隐藏层和给定数量节点的全连接神经网络。函数的输出为一个 2 维向量，对应我们试着去学习的真实数据集的维度。对上面的函数也很容易修改，添加更多隐藏层、不同类型的层、不同的激活和输出映射等。

 

我们用如下函数实现鉴别器网络：

def discriminator(X,hsize=[16, 16],reuse=False):
    with tf.variable_scope("GAN/Discriminator",reuse=reuse):
        h1 = tf.layers.dense(X,hsize[0],activation=tf.nn.leaky_relu)
        h2 = tf.layers.dense(h1,hsize[1],activation=tf.nn.leaky_relu)
        h3 = tf.layers.dense(h2,2)
        out = tf.layers.dense(h3,1)

return out, h3

 

该函数会将输入 placeholder 认作来自真实数据集向量空间的样本，这些样本可能是真实样本，也可能是生成器网络所生成的样本。和上面的生成器网络一样，它也会使用 hsize 和 reuse 为输入。我们在鉴别器中使用 3 个隐藏层，前两个层的大小和输入中一致，将第三个隐藏层的大小修改为 2，这样我们就能在 2 维平面上查看转换后的特征空间，在后面部分会讲到。该函数的输出是给定 X 和最后一层的输出（鉴别器从 X 中学习的特征转换）的 logit 预测（logit 就是神经网络模型中的 W * X矩阵）。该 logit 函数和 S 型函数正好相反，后者常用于表示几率（变量为 1 的概率和为 0 的概率之间的比率）的对数。

 

对抗式训练

出于训练目的，我们将如下占位符 x 和 z 分别定义为真实样本和随机噪声样本：

X = tf.placeholder(tf.float32,[None,2])
Z = tf.placeholder(tf.float32,[None,2])

 

对于从生成器中生成样本以及向鉴别器中输入真实和生成的样本，我们还需要创建出它们的图形。通过使用前面定义的函数和占位符可以做到这一点：

G_sample = generator(Z)
r_logits, r_rep = discriminator(X)
f_logits, g_rep = discriminator(G_sample,reuse=True)

 

使用生成的数据和真实数据的 logit，我们将生成器和鉴别器的损失函数定义如下：

disc_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=r_logits,labels=tf.ones_like(r_logits)) + tf.nn.sigmoid_cross_entropy_with_logits(logits=f_logits,labels=tf.zeros_like(f_logits)))
gen_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=f_logits,labels=tf.ones_like(f_logits)))

 

这些损失是基于 sigmoid 交叉熵的损失，其使用我们前面定义的方程。这种损失函数在离散分类问题中很常见，它将 logit（由我们的鉴别器网络给定）作为输入，为每个样本预测正确的标签，然后会计算每个样本的误差。我们使用的是 TensorFlow 中实现的该种损失函数逇优化版，比直接计算交叉熵更加稳定。更多详情可以看看相关 TensorFlow API：

https://www.tensorflow.org/api_docs/python/tf/nn/sigmoid_cross_entropy_with_logits

 

接下来，我们用上面所述的损失函数和生成器及鉴别器网络函数中定义的网络层范围，定义这两个网络的优化器。在两个神经网络中我们使用 RMSProp 优化器，学习率设为 0.001，范围则为我们只为给定网络所获取的权重或变量。

gen_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,scope="GAN/Generator")
disc_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,scope="GAN/Discriminator")

gen_step = tf.train.RMSPropOptimizer(learning_rate=0.001).minimize(gen_loss,var_list = gen_vars) # G Train step
disc_step = tf.train.RMSPropOptimizer(learning_rate=0.001).minimize(disc_loss,var_list = disc_vars) # D Train step

 

然后我们按照所需数量的步骤训练这两个网络：

for i in range(100001):
    X_batch = sample_data(n=batch_size)
    Z_batch = sample_Z(batch_size, 2)
    _, dloss = sess.run([disc_step, disc_loss], feed_dict={X: X_batch, Z: Z_batch})
    _, gloss = sess.run([gen_step, gen_loss], feed_dict={Z: Z_batch})

print "Iterations: %dt Discriminator loss: %.4ft Generator loss: %.4f"%(i,dloss,gloss)

 

可以对上面的代码进行修改，获得更复杂的训练过程，比如为鉴别器或生成器更新运行多个步骤，获取真实和生成的样本的特征，绘制生成的样本。这里的操作可以参考我的代码库。

 

分析GAN

可视化训练损失

 

为了能更好地理解训练过程，我们可以每 10 次迭代后就绘制出训练损失。从下图中我们可以看到损失逐渐下降，到了训练末尾几乎保持不变。当鉴别器和生成器网络的损失达到这种几乎不再变动的状态时，就表示模型达到了平衡状态。

 

 

 

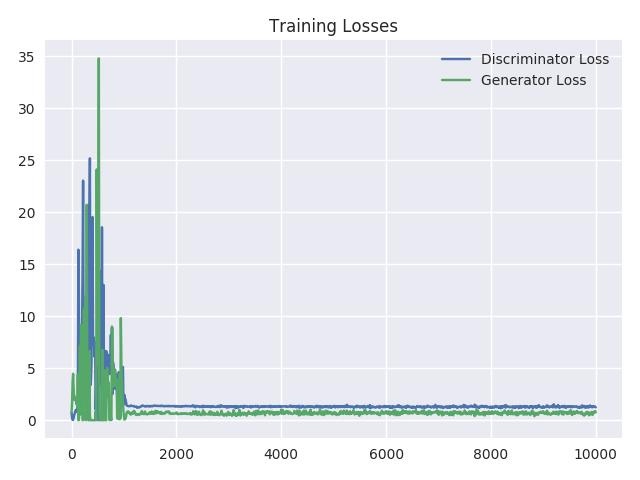
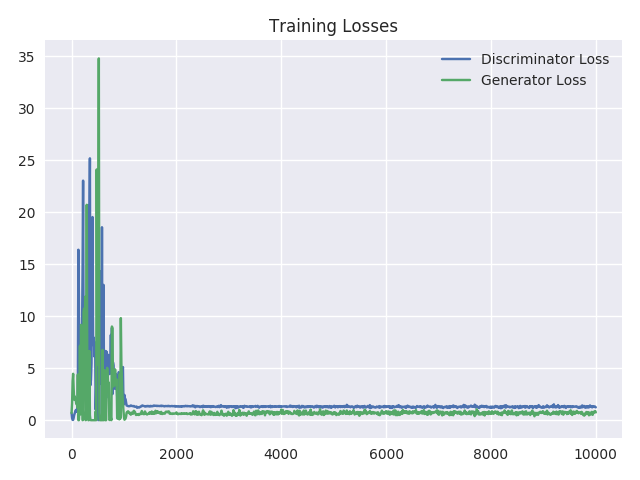
可视化训练期间的样本

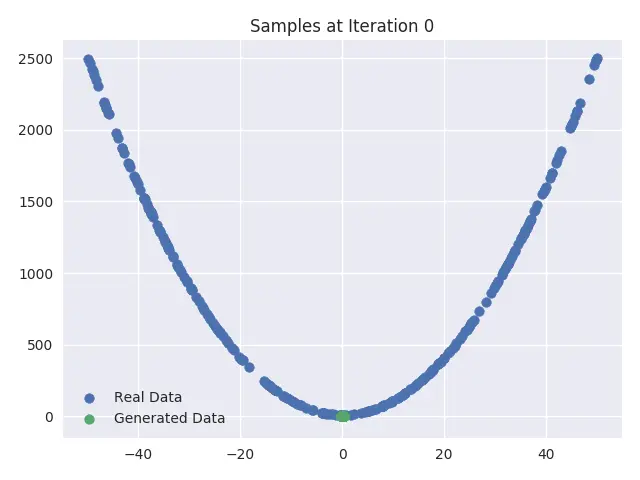
我们还可以在训练中每 1000 次迭代后绘制出真实样本和生成的样本，这些可视化图能清晰地展现生成器网络首先以输入和数据集向量空间的随机初始映射开始，然后慢慢发展至模拟真实数据集样本。你可以看到，“虚假”样本开始看起来越来越像“真实”数据分布。

 

 

 

可视化生成器更新

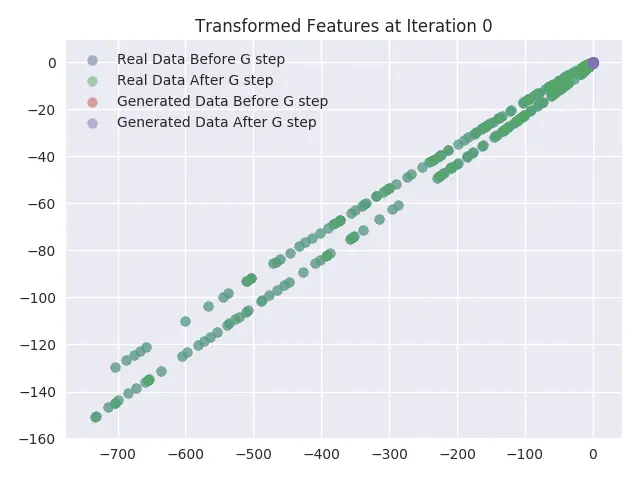
在这部分，我们将对抗式训练期间更新生成器网络权重的影响进行可视化。通过绘制鉴别器网络最后一个隐藏层的激活状况完成这一步。我们将最后一个隐藏层大小设置为 2，这样就能在无需降维（即将输入样本转换为不同的向量空间）的情况下很容易地绘制图形。我们对可视化鉴别器网络所学习的特征转换函数很感兴趣，正是这个函数让模型区分真实和虚假数据。

 

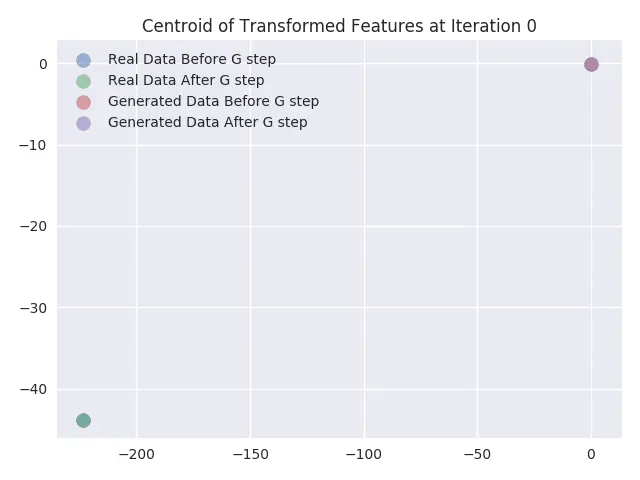
我们绘制出鉴别器网络最后一层学习的真实样本及生成样本的特征准换图形，并且分别绘出更新生成器网络的权重之前和之后两种情况的图形。另外还绘制出在输入样本的特征转换后获取的数据点的形心（centroid）。最后，我们分别计算真实数据和虚假数据的数据点形心，以及更新生成器之间和之后的数据点形心。从可视化图形中可以发现如下现象：

 

• 和预期一样，真实数据样本的转换特征并没有出现变化。从图形中可以看到它们完全一致。
• 从形心可视化图中可以看到，生成的数据样本的特征形心几乎和真实数据样本的特征形心走势一致。
• 还可以看到，随着迭代次数增加，真实样本的转换特征混入越来越多的生成样本的转换特征。这也在预期之内，因为在训练鉴别器网络末尾时，应该就无法区分真实样本和生成样本。因此，在训练结束时，这两种样本的转换特征应当一致。

 

 

 

 

 

结语

本文我们用 TensorFlow 实现了一种概念验证 GAN 模型，能从非常简单的数据分布中生成数据。在你自己练习时，建议将文中代码进行如下调整：

 

• 对鉴别器更新之前和之后的情况进行可视化
• 改变各个层级的激活函数，看看训练和生成样本的区别
• 添加更多层以及不同类型的层，看看对训练时间和训练稳定性的影响
• 调整代码以生成数据，包含来自两个不同曲线的数据
• 调整以上代码，能够处理更复杂的数据，比如 MNIST，CIFAR-10，等等。