一、卷积神经网络参数计算
CNN一个牛逼的地方就在于通过感受野和权值共享减少了神经网络需要训练的参数的个数,所谓权值共享就是同一个Feature Map中神经元权值共享,该Feature Map中的所有神经元使用同一个权值。因此参数个数与神经元的个数无关,只与卷积核的大小及Feature Map的个数相关。但是共有多少个连接个数就与神经元的个数相关了,神经元的个数也就是特征图的大小。
下面以最经典的LeNet-5例子来逐层分析各层的参数及连接个数。
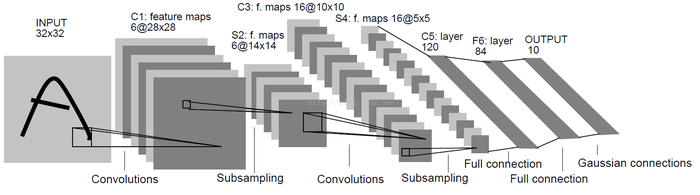
C1层是一个卷积层,由6个特征图Feature Map构成。特征图中每个神经元与输入为5*5的邻域相连。特征图的大小为28*28,这样能防止输入的连接掉到边界之外(32-5+1=28)。C1有156个可训练参数(每个滤波器5*5=25个unit参数和一个bias参数,一共6个滤波器,共(5*5+1)*6=156个参数),共156*(28*28)=122,304个连接。
S2层是一个下采样层,有6个14*14的特征图。特征图中的每个单元与C1中相对应特征图的2*2邻域相连接。S2层每个单元的4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。每个单元的2*2感受野并不重叠,因此S2中每个特征图的大小是C1中特征图大小的1/4(行和列各1/2)。S2层有12(6*(1+1)=12)个可训练参数和5880(14*14*(2*2+1)*6=5880)个连接。
C3层也是一个卷积层,它同样通过5x5的卷积核去卷积层S2,然后得到的特征map就只有10x10个神经元,但是它有16种不同的卷积核,所以就存在16个特征map了。 C3中每个特征图由S2中所有6个或者几个特征map组合而成。为什么不把S2中的每个特征图连接到每个C3的特征图呢?原因有2点。第一,不完全的连接机制将连接的数量保持在合理的范围内。第二,也是最重要的,其破坏了网络的对称性。由于不同的特征图有不同的输入,所以迫使他们抽取不同的特征(希望是互补的)。
例如,存在的一个方式是:C3的前6个特征图以S2中3个相邻的特征图子集为输入。接下来6个特征图以S2中4个相邻特征图子集为输入。然后的3个以不相邻的4个特征图子集为输入。最后一个将S2中所有特征图为输入。这样C3层有1516(6*(3*25+1)+6*(4*25+1)+3*(4*25+1)+(25*6+1)=1516)个可训练参数和151600(10*10*1516=151600)个连接。
S4层是一个下采样层,由16个5*5大小的特征图构成。特征图中的每个单元与C3中相应特征图的2*2邻域相连接,跟C1和S2之间的连接一样。S4层有32个可训练参数(每个特征图1个因子和一个偏置16*(1+1)=32)和2000(16*(2*2+1)*5*5=2000)个连接。
C5层是一个卷积层,有120个特征图。每个单元与S4层的全部16个单元的5*5邻域相连。由于S4层特征图的大小也为5*5(同滤波器一样),故C5特征图的大小为1*1(5-5+1=1):这构成了S4和C5之间的全连接。之所以仍将C5标示为卷积层而非全相联层,是因为如果LeNet-5的输入变大,而其他的保持不变,那么此时特征图的维数就会比1*1大。C5层有48120(120*(16*5*5+1)=48120由于与全部16个单元相连,故只加一个偏置)个可训练连接。
F6层有84个单元(之所以选这个数字的原因来自于输出层的设计),与C5层全相连。有10164(84*(120*(1*1)+1)=10164)个可训练参数。如同经典神经网络,F6层计算输入向量和权重向量之间的点积,再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个状态。
最后,输出层由欧式径向基函数(Euclidean Radial Basis Function)单元组成,每类一个单元,每个有84个输入。
二、神经网络时间复杂度和空间复杂度(参数量计算和计算量计算)



三、卷积层输出尺寸计算
先定义几个参数
- 输入图片大小 W×W
- Filter大小 F×F
- 步长 S
- padding的像素数 P
则输出为N*N,其中N = (W − F + 2P )/S+1。具体计算如下:
卷积中的特征图大小计算方式有两种,分别是‘VALID’和‘SAME’,卷积和池化都适用,除不尽的结果都向上取整。
1.如果计算方式采用'VALID',则:
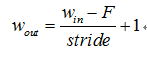
其中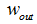 为输出特征图的大小,
为输出特征图的大小,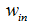 为输入特征图的大小,F为卷积核大小,stride为卷积步长。
为输入特征图的大小,F为卷积核大小,stride为卷积步长。
2.如果计算方式采用'SAME',输出特征图的大小与输入特征图的大小保持不变,

其中padding为特征图填充的圈数。若采用'SAME'方式,kernel_size=1时,padding=0;kernel_size=3时,padding=1;kernel_size=5时,padding=3,以此类推。
转自:
https://blog.csdn.net/gloriazhang2013/article/details/71426871
https://blog.csdn.net/gubenpeiyuan/article/details/81561262
https://blog.csdn.net/HelloZEX/article/details/81109136
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:卷积神经网络参数计算及卷积层输出尺寸计算 - Python技术站

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫