循环神经网络（学习笔记）

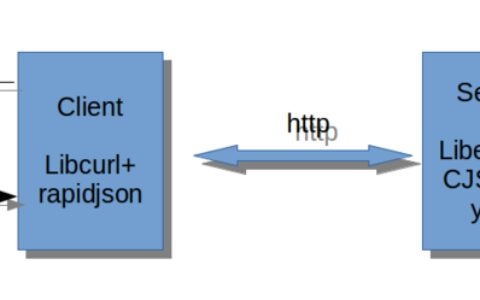
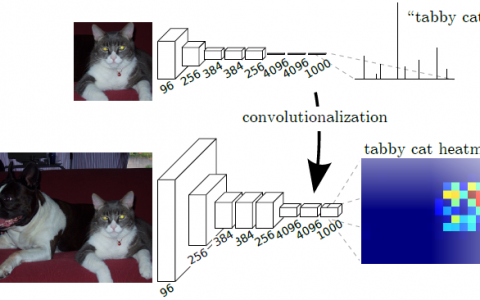
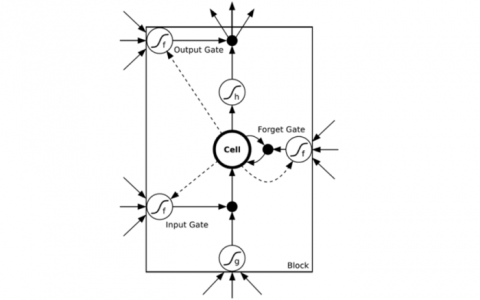
简单的是语言的概率模型，根据前面的单词推断下一个单词。
$p(word_i|word_1,...,word_{i-1})$

2-gram LM Model

两个词作为输入向量，$w_i|w_{i-1}, w_{i-2}~ p_i(w_i|w_{i-1},w_{i-2})$

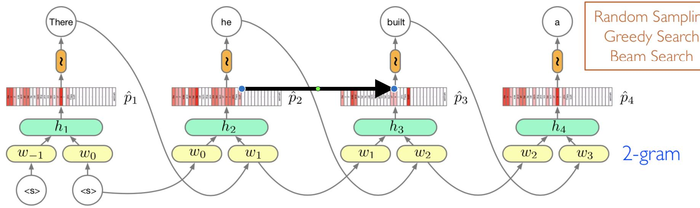
同样会出现参数的爆炸，序列的长度决定MLP的长度。很难扩展到long-term的模型。MLP网络中参数不是共享的，但是在RNN网络中参数是共享的。

RNN

RNN时间上的局部依赖，对比CNN网络中空间的局部依赖。
$p(x_1,...,x_T) = \prod_{t=1}^{T}p(x_t|x_1,...x_{t-1})=\prod_{t=1}^Tg(s_{t-2}, x_{t-1})$
但是上面的联合概率分布的计算的复杂度是($d^T$).
一阶马尔可夫：T=2

• 假设1:$s_{t-2}$代表将前面的概率编码到隐变量中，这就是循环神经网络的局部依赖假设。

• 假设2: 参数共享
  $p(x_{t_1+\tau},..., x_{t_n + \tau}) = P(x_{t_1},..., x_{t_n})$时间平移的平稳性。平稳性假设是需要的，不然RNN无法建模，如果没有平稳性假设，变量的数据无法对应到网络的输入。
  

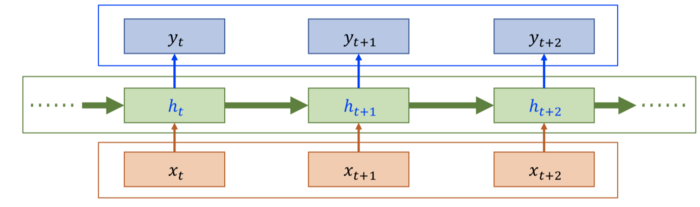
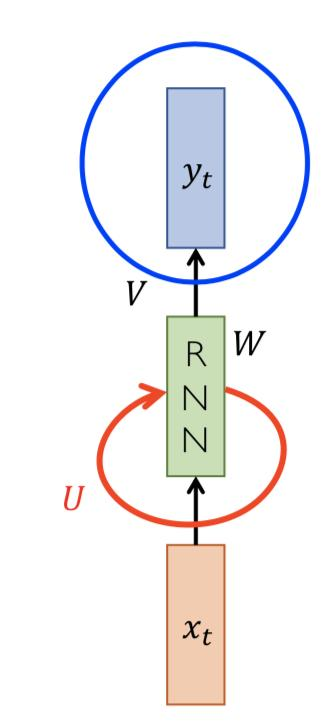
重要的公式：
$y_t = Vh_t$这里是线性的变化，也可以在分类的时候使用softmax。

$h_t = f_W(h_{t-1}, x_t) -> h_t = tanh(Wh_{t-1}+Ux_t)$ 这里的+ 代表concat 操作。

深度循环神经网络

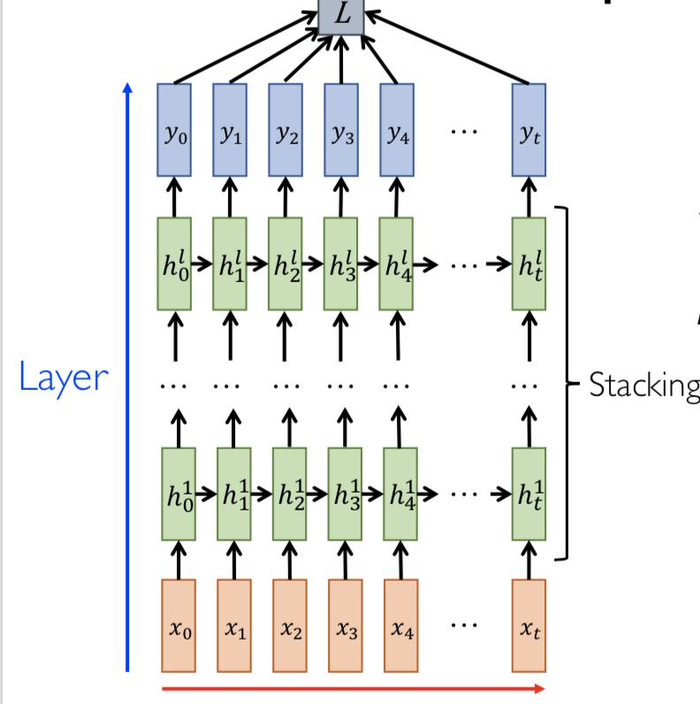
$\hat{y_t} = softmax(Vh_t^l)$

时间上的循环$h_t^1 = tanh(W_1h_{t-1}^1+U_1x_t)$

层次之间的循环 $h_t^l = tanh(W_lh_{t-1}+U_lh_t^{l-1})$

分类问题：损失函数（cross-entroy）:
$L=-\frac{1}{T}\sum_{t=1}^T\sum_{c=1}^Cy_{t,c}log(\hat{y_{t,c}})$

回归问题采用：L1, L2损失函数。
L1损失函数 $L=\sum_{i=1}^n(Y_i - f(y_i))$

L2损失函数：$L=\sum_{i=1}^n(Y_i - f(y_i))^2$

双向循环网络（Bidirectional RNN）

Bert等大规模的循环网络仍然有采用双向循环网络。

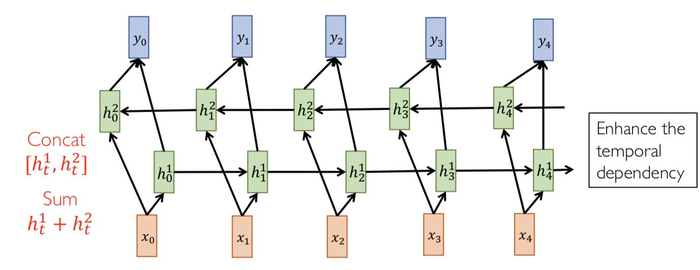
优点

1.循环网络在时序依赖上是无界的。
2.历史的信息编码到固定的长度。
3.参数打小不随着序列的长度变化。

缺点

很难建模长时间的依赖关系。例如时间上相邻很远的输入之间的关系。