吴恩达《卷积神经网络》课程笔记（1）– 卷积神经网络基础

1. Computer Vision
计算机视觉是深度学习应用的主要方向之一。一般的CV问题包括以下三类：

Image Classification图像分类，Object detection目标检测，Neural Style Transfer图片风格迁移

下图展示了一个Neural Style Transfer的例子：

 

使用传统神经网络处理计算机视觉的一个主要问题是输入层维度很大。例如一张64x64x3的图片，神经网络输入层的维度为12288。如果图片尺寸较大，例如一张1000x1000x3的图片，神经网络输入层的维度将达到3百万，使得网络权重W非常庞大。这样会造成两个后果，一是神经网络结构复杂，数据量相对不够，容易出现过拟合；二是所需内存、计算量较大。解决这一问题的方法就是使用卷积神经网络（CNN）。

2. Edge Detection Example边缘检测示例
最常检测的图片边缘有两类：一是垂直边缘（vertical edges），二是水平边缘（horizontal edges）。

 图片的边缘检测可以通过与相应滤波器进行卷积来实现。以垂直边缘检测为例，原始图片尺寸为6x6，滤波器filter尺寸为3x3，卷积后的图片尺寸为4x4，得到结果如下：

 

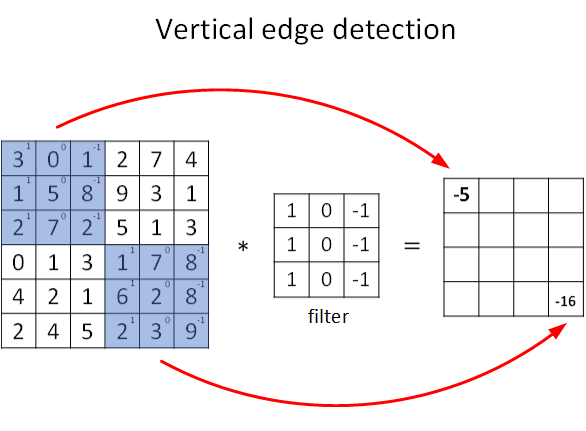
上图只显示了卷积后的第一个值和最后一个值。

图中∗表示卷积操作。

python中，卷积用conv_forward()表示；

tensorflow中，卷积用tf.nn.conv2d()表示；

keras中，卷积用Conv2D()表示。

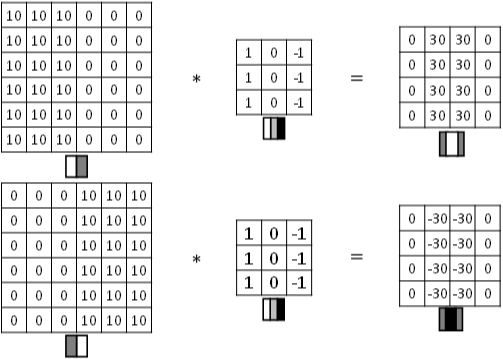
Vertical edge detection能够检测图片的垂直方向边缘。下图对应一个垂直边缘检测的例子：

 

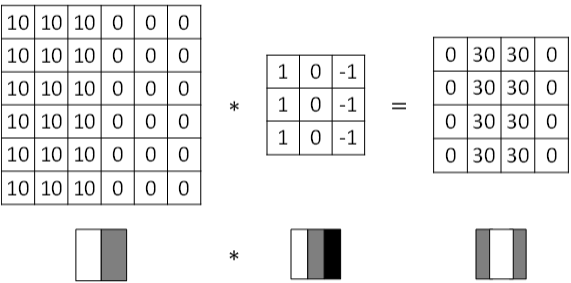
像素值10 是比较亮的像素值，像素值0是比较暗的像素值

卷积运算提供了一个方便的方法来发现图像中的垂直边缘

3. More Edge Detection更多边缘检测内容
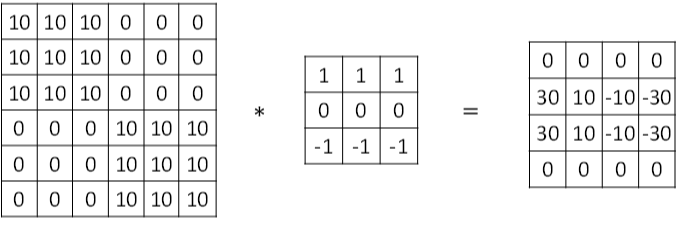
图片边缘有两种渐变方式，一种是由明变暗，另一种是由暗变明。以垂直边缘检测为例，下图展示了两种方式的区别。实际应用中，这两种渐变方式并不影响边缘检测结果，可以对输出图片取绝对值操作，得到同样的结果。

 

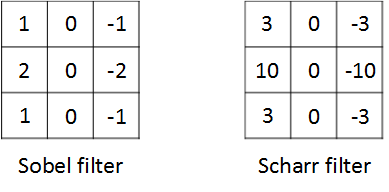
垂直边缘检测和水平边缘检测的滤波器算子如下所示：

 

下图展示一个水平边缘检测的例子：

 

除了上面提到的这种简单的Vertical、Horizontal滤波器之外，还有其它常用的filters，例如Sobel filter和Scharr filter。这两种滤波器的特点是增加图片中心区域的权重。

 

上图展示的是垂直边缘检测算子，水平边缘检测算子只需将上图顺时针翻转90度即可。

在深度学习中，如果我们想检测图片的各种边缘特征，而不仅限于垂直边缘和水平边缘，那么filter的数值一般需要通过模型训练得到，类似于标准神经网络中的权重W一样由梯度下降算法反复迭代求得。CNN的主要目的就是计算出这些filter的数值。确定得到了这些filter后，CNN浅层网络也就实现了对图片所有边缘特征的检测。

4. Padding
按照我们上面讲的图片卷积，如果原始图片尺寸为n x n，filter尺寸为f x f，则卷积后的图片尺寸为(n-f+1) x (n-f+1)，注意f一般为奇数。这样会带来两个问题：

1.卷积运算后，输出图片尺寸缩小

2.原始图片边缘信息对输出贡献得少，输出图片丢失边缘信息

为了解决图片缩小的问题，可以使用padding方法，即把原始图片尺寸进行扩展，扩展区域补零，用p来表示每个方向扩展的宽度。

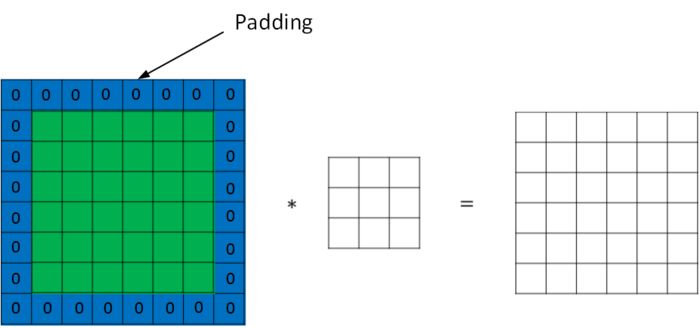
经过padding之后，原始图片尺寸为(n+2p) x (n+2p)，filter尺寸为f x f，则卷积后的图片尺寸为(n+2p-f+1) x (n+2p-f+1)。若要保证卷积前后图片尺寸不变，则p应满足：

p=(f−1)/2
没有padding操作，p=0p=0，我们称之为“Valid convolutions”；有padding操作，p=f−12p=f−12，我们称之为“Same convolutions”。

5. Strided Convolutions卷积步长
Stride表示filter在原图片中水平方向和垂直方向每次的步进长度。之前我们默认stride=1。若stride=2，则表示filter每次步进长度为2，即隔一点移动一次。

 

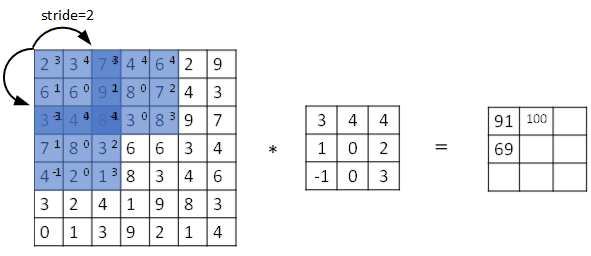
我们用s表示stride长度，p表示padding长度，如果原始图片尺寸为n x n，filter尺寸为f x f，则卷积后的图片尺寸为：

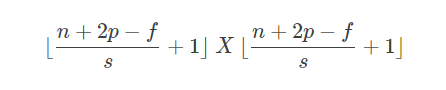
上式中，⌊⋯⌋表示向下取整。

值得一提的是，相关系数（cross-correlations）与卷积（convolutions）之间是有区别的。实际上，真正的卷积运算会先将filter绕其中心旋转180度，然后再将旋转后的filter在原始图片上进行滑动计算。filter旋转如下所示：

 

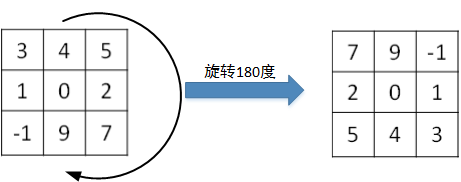
比较而言，相关系数的计算过程则不会对filter进行旋转，而是直接在原始图片上进行滑动计算。

其实，目前为止我们介绍的CNN卷积实际上计算的是相关系数，而不是数学意义上的卷积。但是，为了简化计算，我们一般把CNN中的这种“相关系数”就称作卷积运算。之所以可以这么等效，是因为滤波器算子一般是水平或垂直对称的，180度旋转影响不大；而且最终滤波器算子需要通过CNN网络梯度下降算法计算得到，旋转部分可以看作是包含在CNN模型算法中。总的来说，忽略旋转运算可以大大提高CNN网络运算速度，而且不影响模型性能。

卷积运算服从结合律：

(A∗B)∗C=A∗(B∗C)
6. Convolutions Over Volume卷积为何有效
对于3通道的RGB图片，其对应的滤波器算子同样也是3通道的。例如一个图片是6 x 6 x 3，分别表示图片的高度（height）、宽度（weight）和通道（#channel）。

3通道图片的卷积运算与单通道图片的卷积运算基本一致。过程是将每个单通道（R，G，B）与对应的filter进行卷积运算求和，然后再将3通道的和相加，得到输出图片的一个像素值。

 

不同通道的滤波算子可以不相同。例如R通道filter实现垂直边缘检测，G和B通道不进行边缘检测，全部置零，或者将R，G，B三通道filter全部设置为水平边缘检测。

为了进行多个卷积运算，实现更多边缘检测，可以增加更多的滤波器组。例如设置第一个滤波器组实现垂直边缘检测，第二个滤波器组实现水平边缘检测。这样，不同滤波器组卷积得到不同的输出，个数由滤波器组决定。

 

若输入图片的尺寸为n x n x ncnc，filter尺寸为f x f x ncnc，则卷积后的图片尺寸为(n-f+1) x (n-f+1) x n′cnc′。其中，ncnc为图片通道数目，n′cnc′为滤波器组个数。

7. One Layer of a Convolutional Network单层卷积网络
卷积神经网络的单层结构如下所示：

 

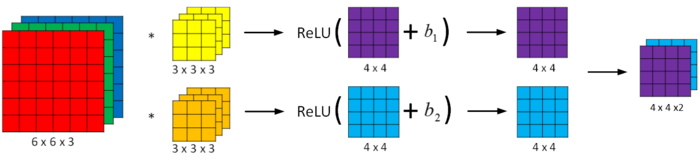
相比之前的卷积过程，CNN的单层结构多了激活函数ReLU和偏移量b。整个过程与标准的神经网络单层结构非常类似：

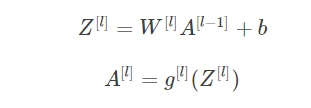
卷积运算对应着上式中的乘积运算，滤波器组数值对应着权重W[l]W[l]，所选的激活函数为ReLU。

我们来计算一下上图中参数的数目：每个滤波器组有3x3x3=27个参数，还有1个偏移量b，则每个滤波器组有27+1=28个参数，两个滤波器组总共包含28x2=56个参数。我们发现，选定滤波器组后，参数数目与输入图片尺寸无关。所以，就不存在由于图片尺寸过大，造成参数过多的情况。例如一张1000x1000x3的图片，标准神经网络输入层的维度将达到3百万，而在CNN中，参数数目只由滤波器组决定，数目相对来说要少得多，这是CNN的优势之一。

最后，我们总结一下CNN单层结构的所有标记符号，设层数为l。

如果有m个样本，进行向量化运算，相应的输出维度为：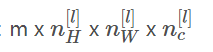

8. Simple Convolutional Network Example简单卷积网络示例
下面介绍一个简单的CNN网络模型：

该CNN模型各层结构如上图所示。需要注意的是，a[3]的维度是7 x 7 x 40，将a[3]排列成1列，维度为1960 x 1，然后连接最后一级输出层。输出层可以是一个神经元，即二元分类（logistic）；也可以是多个神经元，即多元分类（softmax）。最后得到预测输出y^。

CNN有三种类型的layer：

Convolution层（CONV）

Pooling层（POOL）

Fully connected层（FC）

CONV最为常见也最重要，关于POOL和FC我们之后再介绍。

9. Pooling Layers池化层
Pooling layers是CNN中用来减小尺寸，提高运算速度的，同样能减小noise影响，让各特征更具有健壮性。

Pooling layers的做法比convolution layers简单许多，没有卷积运算，仅仅是在滤波器算子滑动区域内取最大值，即max pooling，这是最常用的做法。注意，超参数p很少在pooling layers中使用。

 

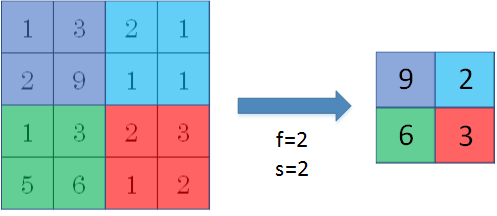
Max pooling的好处是只保留区域内的最大值（特征），忽略其它值，降低noise影响，提高模型健壮性。而且，max pooling需要的超参数仅为滤波器尺寸f和滤波器步进长度s，没有其他参数需要模型训练得到，计算量很小。

如果是多个通道，那么就每个通道单独进行max pooling操作。

除了max pooling之外，还有一种做法：average pooling。顾名思义，average pooling就是在滤波器算子滑动区域计算平均值。

 

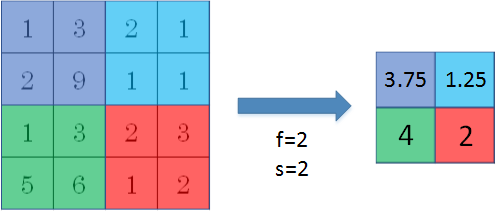
实际应用中，max pooling比average pooling更为常用。

10. CNN Example卷积神经网络示例
下面介绍一个简单的数字识别的CNN例子：

 

 

图中，CON层后面紧接一个POOL层，CONV1和POOL1构成第一层，CONV2和POOL2构成第二层。特别注意的是FC3和FC4为全连接层FC，它跟标准的神经网络结构一致。最后的输出层（softmax）由10个神经元构成。

11. Why Convolutions为什么要使用卷积
相比标准神经网络，CNN的优势之一就是参数数目要少得多。参数数目少的原因有两个：

参数共享：一个特征检测器（例如垂直边缘检测）对图片某块区域有用，同时也可能作用在图片其它区域。

连接的稀疏性：因为滤波器算子尺寸限制，每一层的每个输出只与输入部分区域内有关。

除此之外，由于CNN参数数目较小，所需的训练样本就相对较少，从而一定程度上不容易发生过拟合现象。而且，CNN比较擅长捕捉区域位置偏移。也就是说CNN进行物体检测时，不太受物体所处图片位置的影响，增加检测的准确性和系统的健壮性。