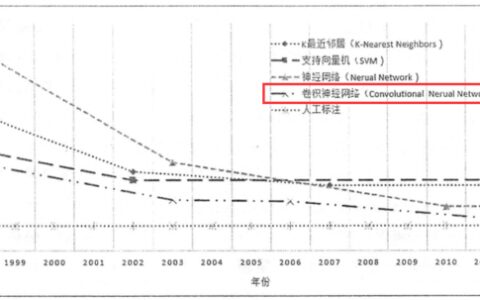
本文为“SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS”, 作者ThomasN.Kipf。
本文是基于谱的图卷积网络用来解决半监督学习的分类问题,输入为图的邻接矩阵A,和每一个节点的特征向量H
本问对应的代码为 https://github.com/tkipf/gcn.
半监督学习主要是cross entropy 损失函数的使用,让只用部分样本也能达到在全部样本的作用下更新参数的效果。
1. 图上谱卷积
A为邻接矩阵, 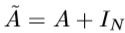 ,D为矩阵A的对角矩阵,
,D为矩阵A的对角矩阵,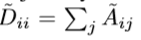 ,Hl 为当前层输入,H(l+1)为当前层输出。
,Hl 为当前层输入,H(l+1)为当前层输出。
我们定义图上的谱卷积为: 一个信号X 乘以 一个过滤器 gtheta = diag(theta), 这个过滤器含有傅里叶阈内的参数theta。
2. 例子
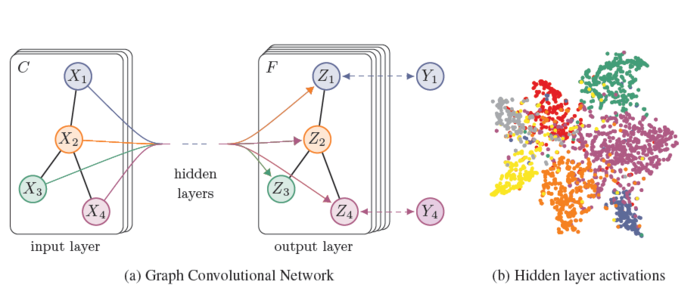
假设我们使用一个两层的GCN的半监督节点分类,假设输入为对称的邻接矩阵A(整数或者小数都行),每个结点的特征向量X.(最好邻接矩阵里面的信息不包含在data X中)
以一个两层的GCN为例子。
首先计算 , 其中A~为A+I, I为单位矩阵, D为A~的对角矩阵。
, 其中A~为A+I, I为单位矩阵, D为A~的对角矩阵。
两层的更新,第一层用Relu更新,第二层用softmax激活函数。
正向传播使用所有的样本, 损失函数用cross-entropy error, 损失函数计算只使用所有label部分,反向传播使用梯度下降。
因为正向传播使用所有的样本,而计算cross function 只使用了label部分,而在反向传播的时候,做梯度下降的时候又使用了所有的样本的值做更新,所以叫做半监督学习。
其中只有coss function使用了label样本。
半监督学习主要是cross entropy 损失函数的使用,让只用部分样本也能达到在全部样本的作用下更新参数的效果。
Cross entropy 的计算公式。
3. 基于图的表示的半监督学习(semi-supervised learning using graph representations)
主要分为两类:
(1)基于图拉普拉斯正则化的方法
(2)Graph embedding-based 方法
4. Node embeddings with random weight
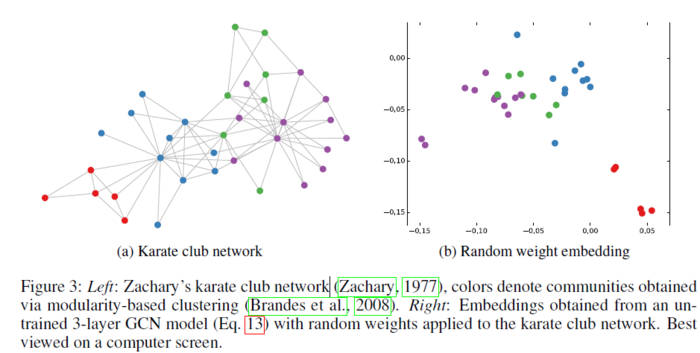
著名的Zachary的空手道俱乐部的例子,使用3层GCN模型, 每层使用随机权重。
由下图可以看到,随机的权重值也可以给点很好的分开,非常的神奇。
本站文章如无特殊说明,均为本站原创,如若转载,请注明出处:Paper:基于图卷积神经网络(Graph Convolutional Networks GCN)的半监督分类 - Python技术站


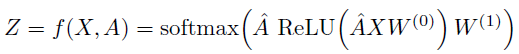
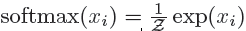

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫