神经网络模型（二）— 卷积神经网络用于知识图谱嵌入（ConvE、ConvKB、R-GCN、ConvR）

目录

• ConvE
  • 模型
    • 问题提出
    • 1D 卷积和 2D 卷积
    • ConvE
  • 实验
    • 数据集
    • Inverse Model
    • 模型参数
    • 链接预测结果
    • 消融实验
  • 代码
• ConvKB
  • 模型
  • 实验
  • 代码
• R-GCN
  • 模型
    • 神经关系建模
    • 实体分类
    • 链接预测
  • 实验
    • 实体分类实验
    • 链接预测
  • 代码
• ConvR
  • 模型
    • 问题提出
    • ConvR
    • loss 与训练
  • 实验
  • 代码

这几篇论文都是用卷积神经网络做知识图谱嵌入的，包括一维、二维卷积、图卷积和自适应卷积，放在一起阅读的。

ConvE

paper: Convolutional 2D Knowledge Graph Embeddings

这篇文章是瑞士大学的 Tim Dettmers 发表在 AAAI 2018 上的工作，文章提出了 ConvE（Convolutional Embedding），用二维卷积网路做 KGE。用各种各样的神经网络做 KG 嵌入的工作从此铺天盖地而来，一开始是卷积、后面有了 attention、胶囊网络等。其实早在 TransE 的时候，就有用神经网络做 KG 表示的，只是不像现在用的网络形式比较多样。

模型

问题提出

文章首先提出链接预测的任务，之前做该任务的模型多是浅层的，相比于深的多层模型，学习特征的能力更弱，因此本文提出了多层的卷积网络 ConvE。

文章重点强调了另一个问题：数据集 WN18 和 FB15k 存在测试集泄露（test set leakage）问题，具体而言就是测试集中的很多三元组样本，是训练集中样本的反向表示（inverse relaitons），这会使得它们很容易被测试成功，因为模型从训练集中学到了它们的相关信息。文章专门针对这个问题做了一些研究实验，甚至专门提出一个模型来处理这类关系。

1D 卷积和 2D 卷积

关于为什么采用 2D 卷积，文章给出的解释是 2D 卷积比 1D 卷积通过 embedding 之间的交互增强了模型的表现力。

1D 卷积对一维的 embedding 做拼接，然后使用 k=3 的过滤器进行卷积，但这样只能捕捉到两个向量拼接点处的交互：

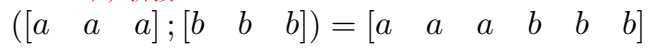
而 2D 卷积将二维的 embedding 进行堆叠，然后用 3x3 的卷积核（过滤器）进行卷积，这样可以捕捉整个拼接行的交互：

总而言之，二维卷积可以比一维卷积抽取更多的特征交互。

ConvE

ConvE 是最简单的用做链接预测的多层卷积网络，组成部分包括一个单层的卷积网，一个投影层和一个内积层。ConvE 不仅参数少，并且通过 1-N 打分的方式加速训练。

打分函数相应定义为：

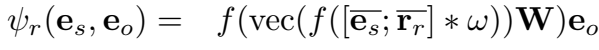
根据模型的架构图，将头实体和关系的向量堆叠，然后 reshape 成二维的张量（类似图像的表示），经过卷积后，得到 feature map，然后经过全连接层投影到 k 维空间中，在内积层与候选目标的 embedding 进行匹配。值得注意的是该模型大量使用 dropout（几乎每一层都用了）。

loss 采用二元交叉熵 loss，优化器采用 Adam：

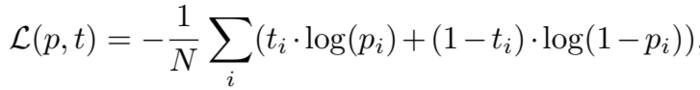
关于采用 1-N 而非 1-1 打分方式提高训练效率的原理，没有整明白=.=。

实验

文章做了大量的实验，不愧是一篇顶会的体量。

数据集

实验使用的数据集包括：WN18(WN18RR)、FB15k(FB15k-237)、YAGO3-10 和 Countries。

Inverse Model

文章构建了简单的、基于规则的模型，该模型自动从训练集中抽取 inverse relations。

模型参数

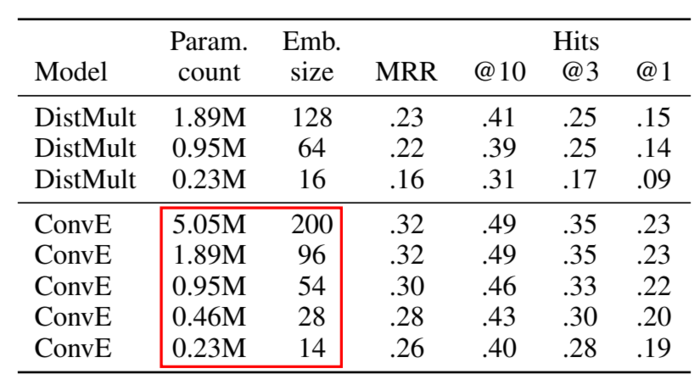
相比于 DistMult，ConvE 参数更少，但效果更好。

链接预测结果

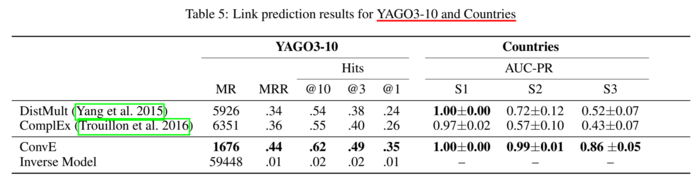
在没有去除 inverse relations 的 WN18 和 FB15k 上，Inverse Model 的效果居然是最好的，而在去除了 inverse relations 的 WN18RR 和 FB15k-237 上，Inverse Model 的效果是最差的，说明 WN18 和 FB15k 确实存在 inverse relation leakage 的问题。因此文章推荐后续的研究尽量选择 WN18RR、FB15k-237 和 YAGO3-10。

消融实验

在 FB15k-237 上进行了消融实验：

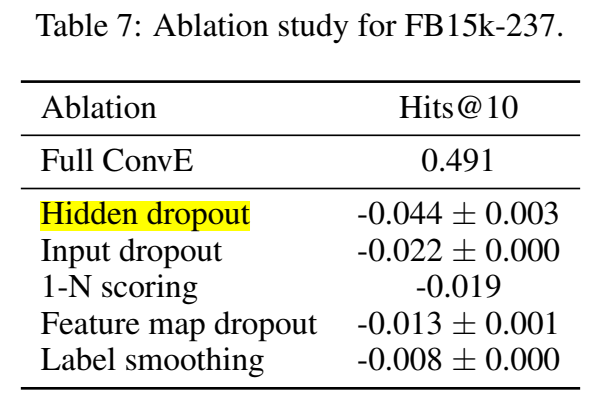
从消融实验结果看出，hidden 层的 dropout 作用最大，label smoothing 作用最无足轻重。

这里解释一下 label smoothing：标签平滑是一种正则化策略，用于防止过拟合；做法是减小真实样本标签类别在计算损失函数时的权重。

代码

文章给出了代码：https://github.com/TimDettmers/ConvE 。试图尝试运行，但是遇到了一点小问题，暂时还没有解决，先放一放。

小结： 文章是用卷积（二维）做 KGE 的开山之作，后面各种网络用于 KGE 也是大势所趋。文章对比的 baseline 不是很多，但做的实验却很多，数据集就用了6个，并且对广泛使用的数据集 WN18 和 FB15k 存在的 test leakage 问题进行了仔细的研究，并给出了实验数据证明。最近看的 NN 做 KGE 的论文都给出了代码，我后面的 idea 应该也会向 NN 这方面靠了。

ConvKB

paper: A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network

这篇论文是澳大利亚迪肯大学的 Dai Quoc Nguyen（好熟悉的名字，之前应该也有看过他的论文）发表在 NAACL 2018 上的文章。文章提出了 ConvKB，虽然比 ConvE 提出的晚，但比 ConvE 稍微降了一个层次：ConvE 是二维卷积，ConvKB 就是普通的一维卷积。而且这两个模型的名字也很容易混淆，都定义的比较泛。ConvKB 是 Convolutional Knowledge Base。整体来说，ConvKB 比 ConvE naive 很多。

模型

文章并没有明确地指出解决的问题，而是直接介绍 CNN：它可以捕捉知识库中的全局关系和翻译的特性。但还是在 Intro 里面小小 diss 了一下 ConvE：它没有关注三元组 embedding \((v_h,v_r,v_t)\) 的相同维度的全局关系，因此忽略了翻译模型的翻译特性。

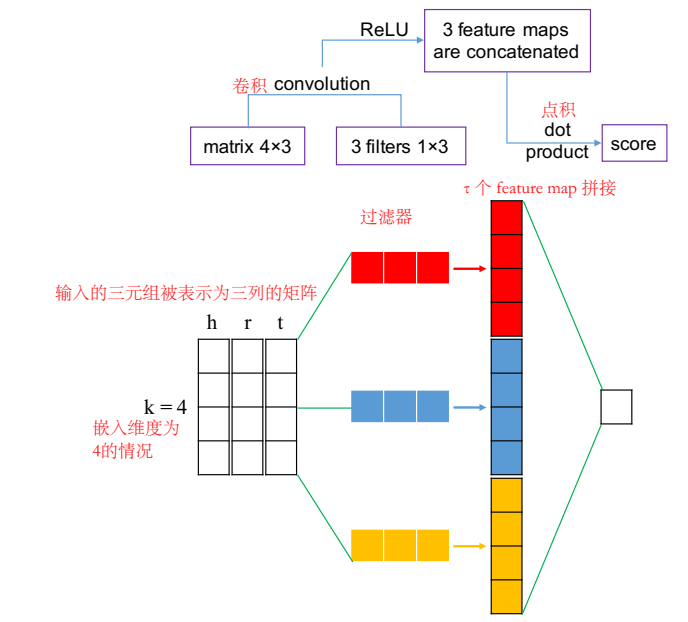
本文提出的 ConvKB 结构：每个三元组表示为一个三列的矩阵，输送到卷积层，多个卷积核对其进行卷积操作输出 feature maps，feature maps 拼接为一个单个的特征向量表示输入，特征向量与一个权重向量相乘，返回三元组得分。

ConvKB 最终的打分函数为：

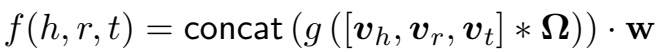
loss 定义为：

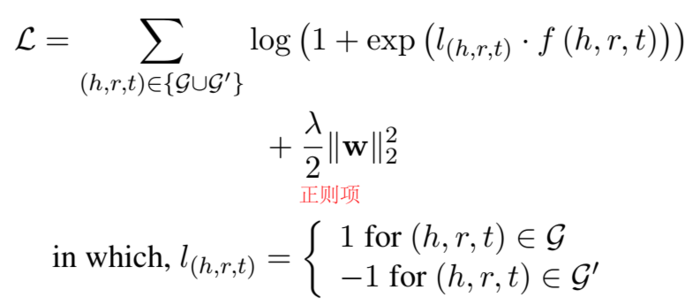
用 Adam 优化器进行训练。

实验

在 WN18RR 和 FB15k 上进行了链接预测实验：

表格最下面四个模型是利用了路径或外部语料信息的模型。

代码

文章中给出了 ConvKB 的代码：https://github.com/daiquocnguyen/ConvKB 。

在 FB15k237 上跑了一下代码，很顺利，得到的结果与论文中和 github 上给的结果差不多。

作者在 github 上给出的实验结果：

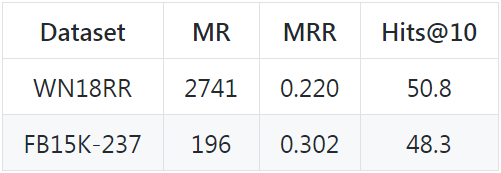
小结： 整体而言，这个模型比较简单，论文体量也比较小，但还是算比较经典的，算是用卷积做 KGE 的最简单的模型了（ConvE 已经不算是最简单的了）。

R-GCN

paper: Modeling Relational Data with Graph Convolutional Networks

这篇文章是荷兰阿姆斯特丹大学的 Michael Schlichtkrull 发表在 ESWC(CCF-C) 2018 上的工作，文章提出了 R-GCN（Relational-Graph Convolutional Network）用于建模关系型数据。该首次提出用图卷积做 KGE，从网上乱飞的论文笔记来看，算是一篇小里程碑式的文章了。只发了 C 可能是因为它的效果不是很好。

模型

文章没有详细介绍所解决的问题，上来直接讲模型。（有的论文比较注重所解决的问题，有的甚至专门设一小节“problem defination”，有的文章却没有）

模型的主体是仿照 GCN 定义了节点的表示，然后具体为不同的任务设计了不同的分类器/编码器/解码器。

神经关系建模

1. 关系图卷积网定义

在看这篇文章之前本想学习一下图卷积的知识，但是都是从傅里叶变换讲起的。但这篇文章的图卷积其实就是一个“信息传播”的思想，用邻居节点的表示作为当前节点的表示，跟 PageRank，还有 PTransE 里面用的那个衡量路径置信度的资源分配算法 PCRA，感觉都差不多=.=。总而言之，图卷积就是用于处理图的神经网络。论文中这么说的：GCN 可以被视为一种简单可微的信息传播框架。

节点 \(v_i\) 在第 \(l+1\) 层的隐状态定义为：

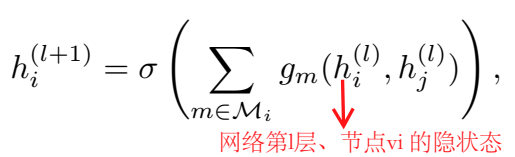
其中，\(M_i\) 代表向节点 \(v_i\) 流入的信息的集合，通常使用入边来代表；\(g_m(\cdot , \cdot)\) 函数用于累积和传递流入的信息，具体可以使用线性变换、ReLU 函数等。

---

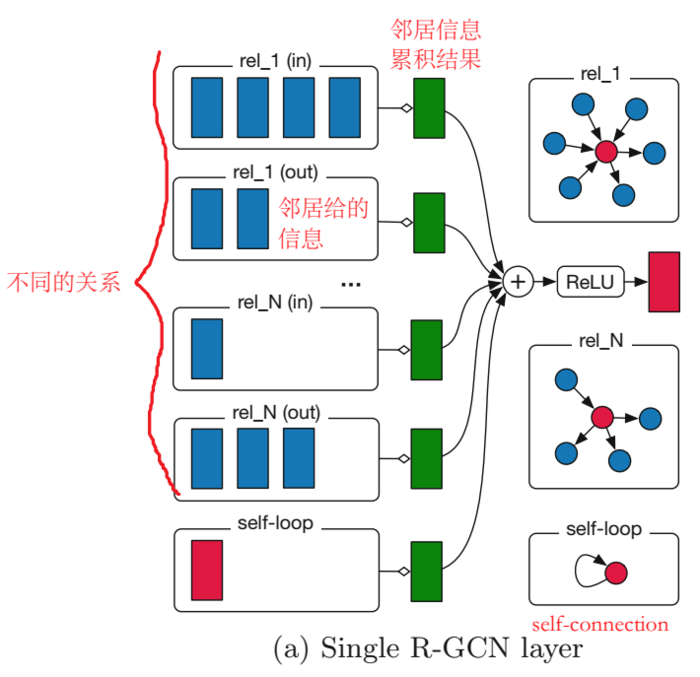
每个节点的表示是上一层的邻居节点表示的加权和和 self-connection 保留一部分自己信息的结果。其实这里的层也可以理解为一个时刻。

仿照 GCN 的架构，为实体中的实体/节点定义了如下的前向传播策略：

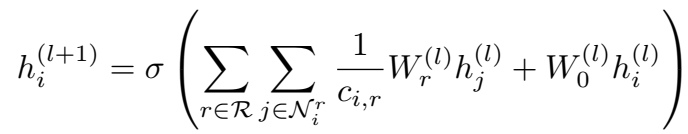
\(N_i^r\) 表示节点 \(v_i\) 在关系 \(r\) 下的邻居节点集合。\(c_{i,r}\) 为归一化常量，通常设置为 \(| N_i^r |\)

2. 正则化

为了防止模型在关系数量较少的情况下过拟合，文章提出了两种正则化方法：

• 基函数分解（basis decomposition）

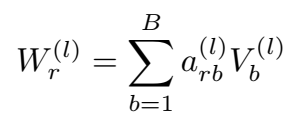
将参数矩阵 \(W_r^{(l)}\) 表示为 \(V_b\) 和 \(a_{rb}\) 的线性组合。

• 块对角分解（block-diagonal decomposition）

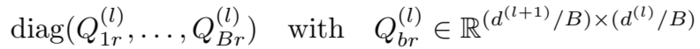
在块对角分解的方法中，将 \(W_r^{(l)}\) 定义为低维矩阵的和，这样得到的 \(W_r^{(l)}\) 是一个块对角矩阵。

两种分解方法都可以减少拟合数据所需要的参数量，同时可以缓解在小样本关系场景下的过拟合。

实体分类

实体分类的任务是判断实体节点所属的类别。在 GCN 的最后一层使用 softmax 激活函数。训练目标为最小化交叉熵 loss：

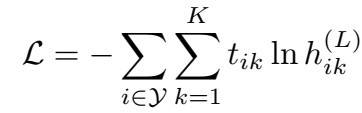
其中，\(h_{ik}^{(L)}\) 表示第 \(i\) 个节点的网络输出的第 \(k\) 个维度的值，\(t_{ik}\) 代表相应的 ground truth label。

链接预测

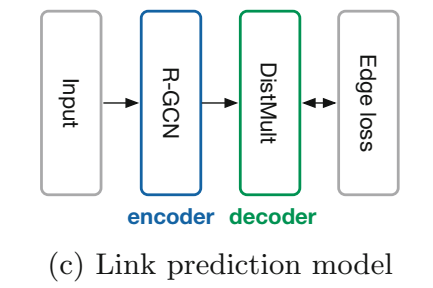
对于链接预测任务，用 R-GCN 编码，得到 embedding，然后用 DistMult 的打分函数计算三元组得分，最后输出交叉熵 loss：

DistMult 打分函数：

交叉熵 loss：

其中，\(l\) 是 logistic sigmoid 函数，\(y\) 是指示样本正负的 indicator。

实验

实体分类实验

用实体分类任务来评估 KGE 效果还是第一次见，使用的数据集也不常见，包括四个：AIFB、MUTAG、BGS、AM。

链接预测

链接预测任务使用的数据集是：WN18、FB15k、FB15k-237。

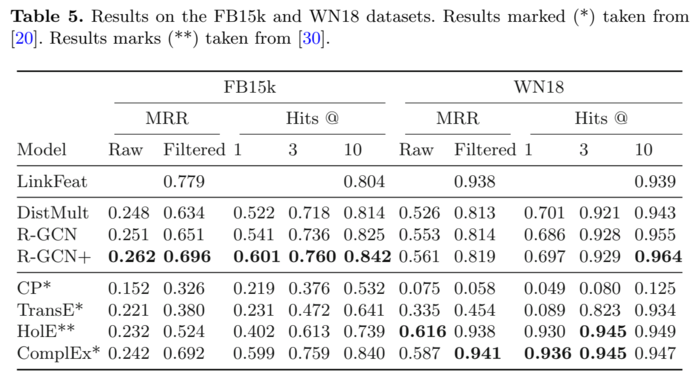
在实验中，R-GCN 的效果提升都比较微弱，但是因为 GCN 的出现，用它来做 KGE 也会是一种必然，所以自然而然会受到关注。

代码

演讲 video 使用的 slides 中给出了实验代码的链接。代码分为了两部分，一作负责的是链接预测的实验，二作（Thomas Kipf）负责的是实体分类的实验。代码项目分别为：https://github.com/MichSchli/RelationPrediction 和 https://github.com/tkipf/relational-gcn 。

链接预测的实验因为 run-trian.py 里面定义的运行环境的路径与当前的代码存放路径不太一样，没有运行成功，暂时先不花时间调了；再、作者在 readme 中说该实验会花费大约几个小时，并且需要一定量的内存。实体分类的实验因为代码中给出的数据集下载链接失效了，遂放弃。

作者演讲 video：http://videolectures.net/eswc2018_kipf_convolutional_networks/ 。

知乎某大佬做的复现：https://zhuanlan.zhihu.com/p/367721297 ，对应 GitHub 项目：https://github.com/lixuanhng/NLP_related_projects/tree/master/GNN/RGCN 。

小结： R-GCN 使用 GCN 的信息传播的思想表示 KG，用上层的卷积输出作为下层的卷积属入，slides 中提到实际是做了 3 层。文章针对实体分类和链接预测任务设计了不同的输出层。KG 本身就是一种图，用 GCN 做 KGE 是理所当然（这里突然想到了 GNN，不知道有没有 GNN for KGE 的工作，R-GCN 是 2018 年的，三年过去了，我想应该有了）。

【题外话——关于论文学习的两点】

1. 找多手资料（paper、code、slides、vedio、别人的笔记等），增进对论文的理解，争取吃透。最近看论文进入了“疲惫期”，厌倦了“看文章-写笔记”的固定模式，常常失去了主动做这件事情的意愿。今天看之前收藏的 R-GCN 笔记的机会，发现了论文原作在会议上讲解论文的视频，看过一遍，虽然没有完全听懂，但也能 get 差不多 50%，而且可以趁机练习英语听力，学习优秀者的表达方式。因此以后看论文（尤其是新论文）时，可以找多手资料加深对论文的理解，缓解固定学习模式带来的疲惫，毕竟比起文字，大脑对于图片和视频的刺激更为敏感。

2. 打破舒适圈，英文表达很重要，多看论文 video 增进语感。这篇 paper 的演讲汇报足足有 30min，问答环节也有很多提问者在认真地提问，作者也都一一做出了回答。这是一个很棒的 report，作者在节奏、表述方面都把握得很好。又看了这个网站（http://videolectures.net）上的其他会议的视频，看了几个 PAKDD 的几个中国学生的 report，感觉应该是演讲者事先写好了讲稿，照着念的录好的一个 video，也没有问答环节，果然很水。之前很畏惧英文报告这件事情，但看一些不那么好的，就会重新拾起一点信心，如果直接看一个目前无法达到的高度（比如本文的作者演讲），就会很容易放弃。英文演讲这件事情，可能并没有像想象中那么难。做到并不难，做得好才难。 只是“做”的话还是很容易达到的，从“不敢做”到“做”，是迈出的重要的一步，因为走出了自己的舒适圈，突破了自己的能力界限，然后后面的工作就是从“做”向“做得好”的方向发展。最关键的一点就是克服自己内心的恐惧，撕掉给自己打上的“我不行”的固有标签。无论多复杂、多难的事情，只要肯花时间、不急不躁、一点点去做，总会是有希望的。

ConvR

paper: Adaptive Convolution for Multi-Relational Learning

这篇文章是腾讯的一位同学发表在 NAACL 2019 上的一篇工作，指导老师是王斌和王泉老师。文章提出了 ConvR 模型，R 代表 relation，是对 ConvE 做的改进，关系做为卷积核，在实体的表示上进行二维卷积，减少了参数量，丰富了实体-关系间的交互，这种方式称为适应卷积（adaptive convolution）。

模型

问题提出

1D 卷积仅能捕捉向量拼接处的交互，因此 ConvE 使用图像处理领域的 2D 卷积用于获取比 1D 卷积更多的交互，但是 2D 卷积也仅仅能捕捉矩阵堆叠相接行的交互，使得实体-关系间的交互还是不充分。因此，为了最大化实体-关系间的交互，提出了 ConvR 模型， 将关系的 embedding 作为卷积核，对头实体的“image”进行卷积，可以获得实体与关系完全的交互。

ConvR

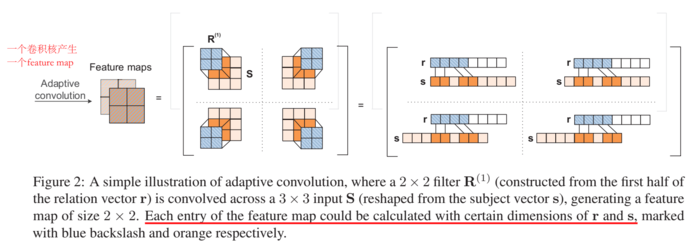
ConvE 中使用的过滤器是外加的 global filter，是固定不变的，而 ConvR 是用关系 emb 代替全局过滤器，对实体的 reshape 进行卷积。具体地，关系 r 的表示分为 c 块，reshape 为 c 个过滤器（卷积核）。卷积的结果就是 feature map，一个卷积核产生一个 feature map，最后所有的 feature map 堆叠为一个向量 \(c\) （不明白为什么堆叠结果是一个向量），与尾实体做点积计算三元组得分。上图中的第二个等号右边的图展示了二维卷积平铺在一维中的表示，可以看出，关系的各部分都与实体的整个表示的各部分都有交互，而不仅仅集中于某些特定的位置。

一个 feature map：

feature map 堆叠后得到的向量 \(c\) 经过一个全连接层，与目标向量（候选尾实体）进行点积，计算出三元组 \((s,r,o)\) 的得分：

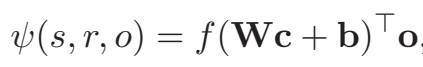
loss 与训练

和 ConvE 一样，使用 1-n 的打分方式加速训练， 使用交叉熵 loss：

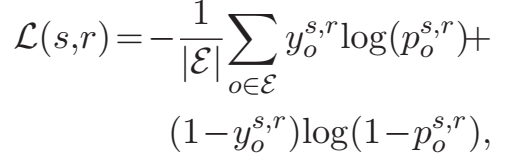
\(y_o^{s,r}\) 是二值标签，指示三元组样本 \((s,r,o)\) 的正负。

和 ConvE 一样，使用 dropout 和 label smoothing 防止过拟合，用 Adam 优化器训练模型。

实验

在四个数据集 WN18、WN18RR、FB15k、FB15k-237 上进行链接预测实验。

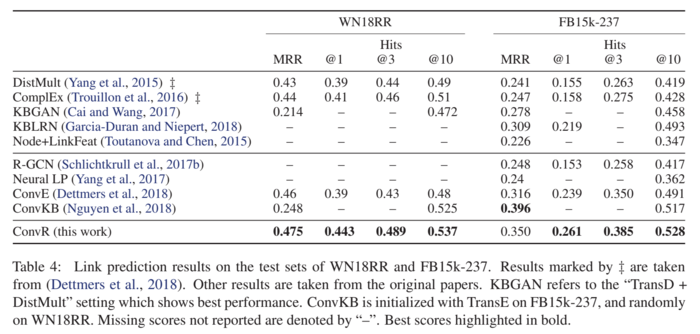
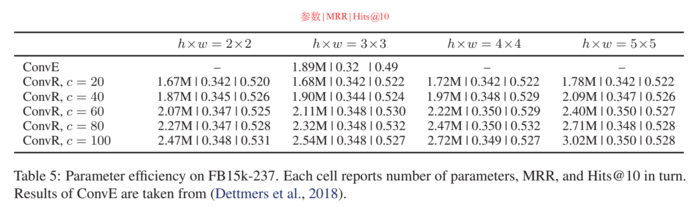
与 ConvR 的参数量及效果对比（在FB15k-237上）：

代码

文章没有给出代码，github 上也没有找到。但是这个模型应当也被视为 NN for KGE 的一个蛮重要的模型。

小结： 最喜欢这种看起来清楚简单的论文和模型，我觉得我又行了[doge]。有两点感悟：1. 模型简单，大概介绍完但又感觉空洞的话，就用符号进行公式化描述，比如关系分块的表示、参数减少具体分析下减少了多少等等。2. 想不出 idea 的话，就做能看懂的文章的 future work。比如这篇文章提出的，可以用 ConvR 做 1D 和 3D 卷积；还可以将实体和关系在卷积操作中的角色互换，实体表示做卷积核，关系表示做 “image”；文章的 conclusion 还提到，应当使尾实体也和关系进行交互。

---

整体小结： ConvE、ConvKB 和 ConvR 都是使用普通的卷积网络，R-GCN 用图卷积，这几篇都是用卷积做 KGE 的工作，再加一篇 GNN 的就好了。几篇看下来，AI 领域的卷积其实就是——“相加再相乘”，至于和通信领域卷积中的“傅里叶变换”的关系，还没太 get 到。

【5.19 早感想】很多模型在效果上并不是碾压式的提升，效果对于论文是否被接收可能只是一方面的因素。所以有了 idea 不必担心后续还未发生的事情，只是去做就好了，一个 idea 必然会对应一篇论文，要做的只是调参训练、调整 baseline 的选择，给出合理的解释等等，只要有模型实现（实验）、结果可以标粗，后续的事情一切就都好办了。