双向循环神经网络、深度循环神经网络、BPTT

循环神经网络

一个简单的循环神经网络，它由输入层、一个隐藏层和一个输出层组成：

 

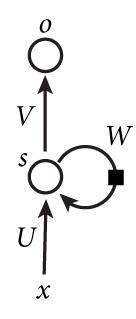
如果把上面有W的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。

x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；

s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；

U是输入层到隐藏层的权重矩阵；

o也是一个向量，它表示输出层的值；

V是隐藏层到输出层的权重矩阵。

那么，现在我们来看看W是什么。

循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。

 

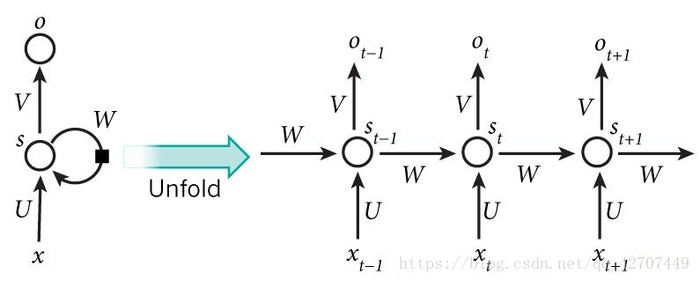
如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：

 

 

 

 

 

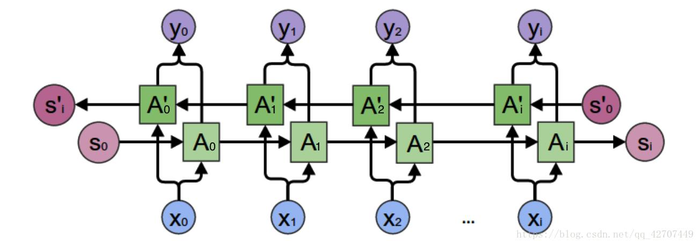
双向循环神经网络

 

我的手机坏了，我打算____一部新手机。

 

 

 

可以想象，如果我们只看横线前面的词，手机坏了，那么我是打算修一修？换一部新的？还是大哭一场？这些都是无法确定的。但如果我们也看到了横线后面的词是『一部新手机』，那么，横线上的词填『买』的概率就大得多了。

基本循环神经网络是无法对此进行建模的，因此，我们需要双向循环神经网络，如下图所示： 

 

 

 

 

深度循环神经网络

 

前面我们介绍的循环神经网络只有一个隐藏层，我们当然也可以堆叠两个以上的隐藏层，这样就得到了深度循环神经网络。如下图所示：

 

 

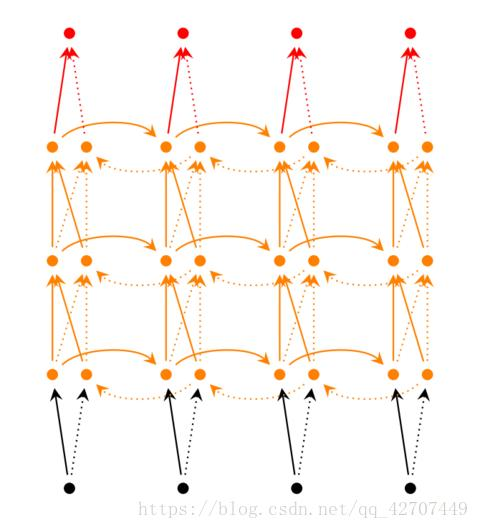
循环神经网络的训练算法：BPTT（back-propagation through time）

BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤： 
1. 前向计算每个神经元的输出值； 
2. 反向计算每个神经元的误差项值，它是误差函数E对神经元j的加权输入的偏导数； 
3. 计算每个权重的梯度。