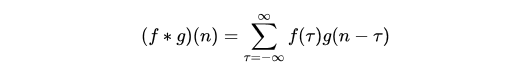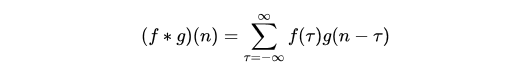对卷积(convolution)的理解
参考文章
https://www.zhihu.com/question/22298352 ----这个是重点
numpy中的一维的卷积
np.convolve([1,2,3,4],[1,1,3],\'full\')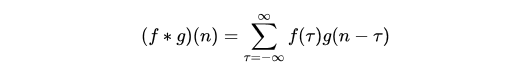 
n m
a（被卷积函数） v（内核）
----------------------------------full-------------------------------------
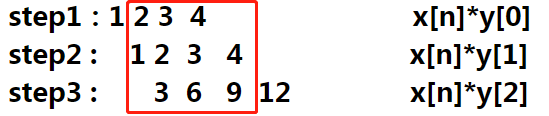
full模式下
step1：1 2 3 4 a[n]*v[0]
step2 : 1 2 3 4 a[n]*v[1]
step3 : 3 6 9 12 a[n]*v[2]
得出卷积的结果是 1 3 8 13 13 12 结果个数是 n+m-1
----------------------------------valid-------------------------------------
valid模式下 数学计算方法
=将 v偏转180度，变成[3，1，1]* [1] [3，1，1]* [2]
[2] [3]
[3] [4]
= [8，13]
如果按照实际意义，就是取完全重合的情况
--------------------------------same-----------------------------------------
same模式下 数学计算方法 ，a前后各补一个0，卷积四次
=将 v偏转180度，变成[3，1，1]* [0] [3，1，1]* [1] [3，1，1]* [2] [3，1，1]* [3]
[1] [2] [3] [4]
[2] [3] [4] [0]
= [3，8，13，13]
如果按照实际意义，就是取有重合的情况
多维的情况类似，对v和a进行，如下变换
卷积过程先将卷积核v旋转180°，被卷积矩阵a扩展到(m+n)*(m+n)大小，将扩展部分用0代替，其序号用负数代替；
本站文章如无特殊说明，均为本站原创，如若转载，请注明出处：对卷积(convolution)的理解 – oliverPP - Python技术站
微信扫一扫 
支付宝扫一扫 